Scleronomous - Alchetron, The Free Social Encyclopedia

A mechanical system is scleronomous if the equations of constraints do not contain the time as an explicit variable. Such constraints are called scleronomic constraints.

Application

Main article：Generalized velocity

In 3-D space, a particle with mass m , velocity v has kinetic energy T

T = 1 2 m v 2 .

Velocity is the derivative of position with respect to time. Use chain rule for several variables:

v = d r d t = ∑ i ∂ r ∂ q i q ˙ i + ∂ r ∂ t .

Therefore,

T = 1 2 m ( ∑ i ∂ r ∂ q i q ˙ i + ∂ r ∂ t ) 2 .

Rearranging the terms carefully,

T = T 0 + T 1 + T 2 : T 0 = 1 2 m ( ∂ r ∂ t ) 2 , T 1 = ∑ i m ∂ r ∂ t ⋅ ∂ r ∂ q i q ˙ i , T 2 = ∑ i , j 1 2 m ∂ r ∂ q i ⋅ ∂ r ∂ q j q ˙ i q ˙ j ,

where T 0 , T 1 , T 2 are respectively homogeneous functions of degree 0, 1, and 2 in generalized velocities. If this system is scleronomous, then the position does not depend explicitly with time:

∂ r ∂ t = 0 .

Therefore, only term T 2 does not vanish:

T = T 2 .

Kinetic energy is a homogeneous function of degree 2 in generalized velocities .

Example: pendulum

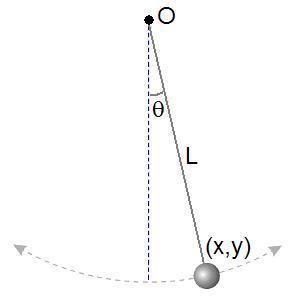
As shown at right, a simple pendulum is a system composed of a weight and a string. The string is attached at the top end to a pivot and at the bottom end to a weight. Being inextensible, the string’s length is a constant. Therefore, this system is scleronomous; it obeys scleronomic constraint

x 2 + y 2 − L = 0 ,

where ( x , y ) is the position of the weight and L is length of the string.

Take a more complicated example. Refer to the next figure at right, Assume the top end of the string is attached to a pivot point undergoing a simple harmonic motion

x t = x 0 cos ⁡ ω t ,

where x 0 is amplitude, ω is angular frequency, and t is time.

Although the top end of the string is not fixed, the length of this inextensible string is still a constant. The distance between the top end and the weight must stay the same. Therefore, this system is rheonomous as it obeys constraint explicitly dependent on time

( x − x 0 cos ⁡ ω t ) 2 + y 2 − L = 0 .

References

Scleronomous Wikipedia

(Text) CC BY-SA

Contents

Application

Example: pendulum

References