 | ||
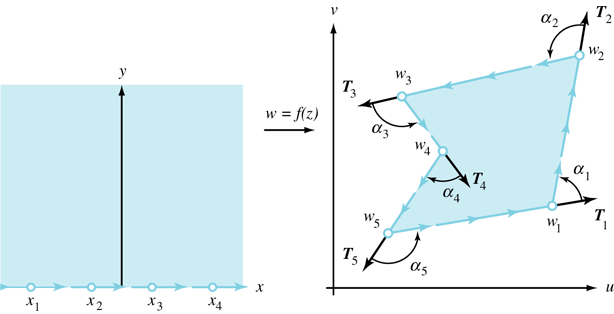
In complex analysis, a Schwarz–Christoffel mapping is a conformal transformation of the upper half-plane onto the interior of a simple polygon. Schwarz–Christoffel mappings are used in potential theory and some of its applications, including minimal surfaces and fluid dynamics. They are named after Elwin Bruno Christoffel and Hermann Amandus Schwarz.
Contents
Definition
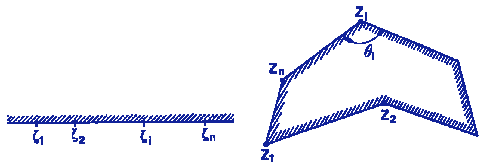
Consider a polygon in the complex plane. The Riemann mapping theorem implies that there is a biholomorphic mapping f from the upper half-plane
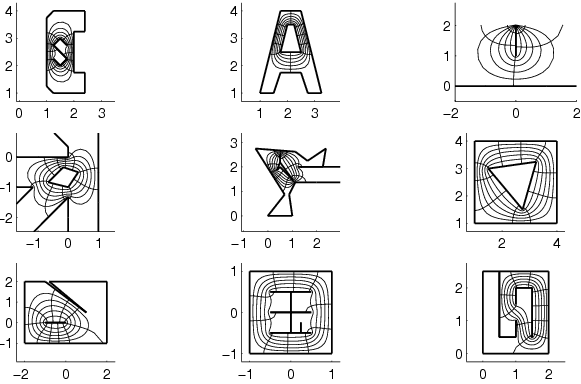
to the interior of the polygon. The function f maps the real axis to the edges of the polygon. If the polygon has interior angles
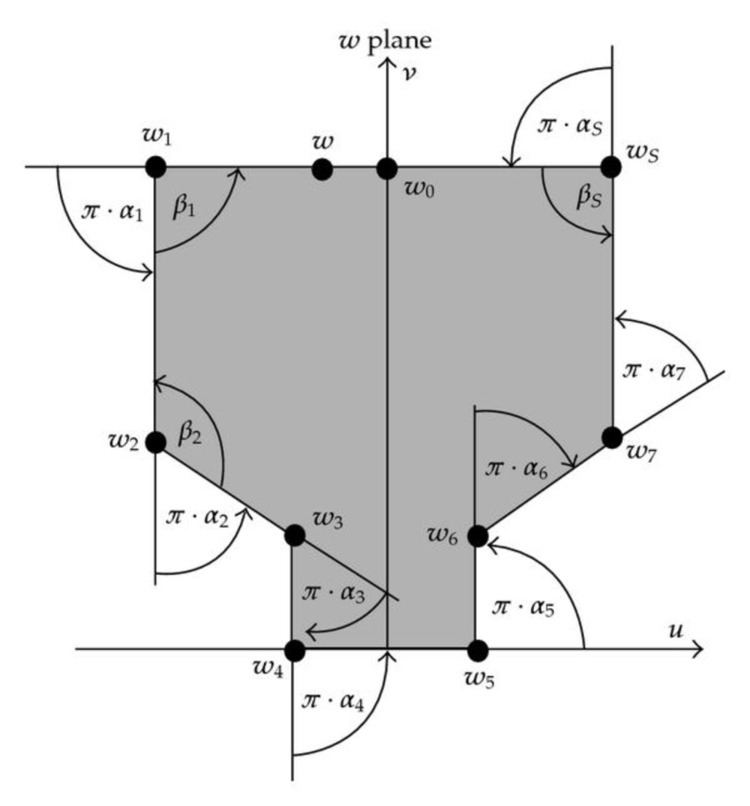
where
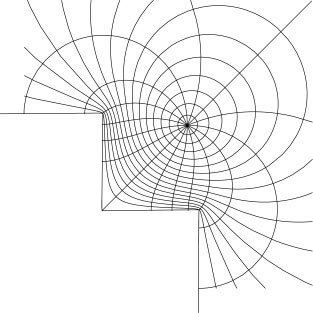
It is often convenient to consider the case in which the point at infinity of the
Example
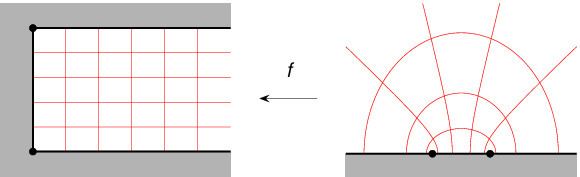
Consider a semi-infinite strip in the z plane. This may be regarded as a limiting form of a triangle with vertices P = 0, Q = π i, and R (with R real), as R tends to infinity. Now α = 0 and β = γ = π⁄2 in the limit. Suppose we are looking for the mapping f with f(−1) = Q, f(1) = P, and f(∞) = R. Then f is given by
Evaluation of this integral yields
where C is a (complex) constant of integration. Requiring that f(−1) = Q and f(1) = P gives C = 0 and K = 1. Hence the Schwarz–Christoffel mapping is given by
This transformation is sketched below.
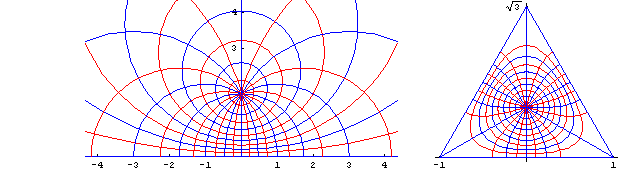
Triangle
A mapping to a plane triangle with angles
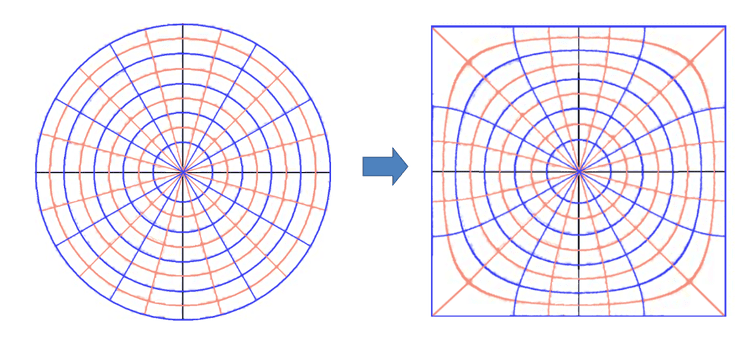
Square
The upper half-plane is mapped to the square by
where F is the incomplete elliptic integral of the first kind.
General triangle
The upper half-plane is mapped to a triangle with circular arcs for edges by the Schwarz triangle map.
