Schur–Horn theorem

Statement

Theorem. Let d = { d i } i = 1 N and λ = { λ i } i = 1 N be vectors in R N such that their entries are in non-increasing order. There is a Hermitian matrix with diagonal values { d i } i = 1 N and eigenvalues { λ i } i = 1 N if and only if

and

Permutation polytope generated by a vector

The permutation polytope generated by x ~ = ( x 1 , x 2 , … , x n ) ∈ R n denoted by K x ~ is defined as the convex hull of the set { ( x π ( 1 ) , x π ( 2 ) , … , x π ( n ) ) ∈ R n : π ∈ S n } . Here S n denotes the symmetric group on { 1 , 2 , … , n } . The following lemma characterizes the permutation polytope of a vector in R n .

Lemma. If x 1 ≥ x 2 ≥ ⋯ ≥ x n , y 1 ≥ y 2 ≥ ⋯ ≥ y n , and x 1 + x 2 + ⋯ + x n = y 1 + y 2 + ⋯ + y n , then the following are equivalent :

(i) ( y 1 , y 2 , ⋯ , y n ) ( = y ~ ) ∈ K x ~ .

(ii) y 1 ≤ x 1 , y 1 + y 2 ≤ x 1 + x 2 , … , y 1 + y 2 + ⋯ + y n − 1 ≤ x 1 + x 2 + ⋯ + x n

(iii) There are points ( x 1 ( 1 ) , x 2 ( 1 ) , ⋯ , x n ( 1 ) ) ( = x ~ 1 ) , … , ( x 1 ( n ) , x 2 ( n ) , … , x n ( n ) ) ( = x ~ n ) in K x ~ such that x ~ 1 = x ~ , x ~ n = y ~ , and x ~ k + 1 = t x ~ k + ( 1 − t ) τ ( x k ~ ) for each k in { 1 , 2 , … , n − 1 } , some transposition τ in S n , and some t in [ 0 , 1 ] , depending on k .

Reformulation of Schur–Horn theorem

In view of the equivalence of (i) and (ii) in the lemma mentioned above, one may reformulate the theorem in the following manner.

Theorem. Let d = { d i } i = 1 N and λ = { λ i } i = 1 N be real vectors. There is a Hermitian matrix with diagonal entries { d i } i = 1 N and eigenvalues { λ i } i = 1 N if and only if the vector ( d 1 , d 2 , … , d n ) is in the permutation polytope generated by ( λ 1 , λ 2 , … , λ n ) .

Note that in this formulation, one does not need to impose any ordering on the entries of the vectors d and λ .

Proof of the Schur–Horn theorem

Let A ( = a j k ) be a n × n Hermitian matrix with eigenvalues { λ i } i = 1 n , counted with multiplicity. Denote the diagonal of A by a ~ , thought of as a vector in R n , and the vector ( λ 1 , λ 2 , … , λ n ) by λ ~ . Let Λ be the diagonal matrix having λ 1 , λ 2 , … , λ n on its diagonal.

( ⇒ ) A may be written in the form U Λ U − 1 , where U is a unitary matrix. Then

Let S = ( s i j ) be the matrix defined by s i j = | u i j | 2 . Since U is a unitary matrix, S is a doubly stochastic matrix and we have a ~ = S λ ~ . By the Birkhoff–von Neumann theorem, S can be written as a convex combination of permutation matrices. Thus a ~ is in the permutation polytope generated by λ ~ . This proves Schur's theorem.

( ⇐ ) If a ~ occurs as the diagonal of a Hermitian matrix with eigenvalues { λ i } i = 1 n , then t a ~ + ( 1 − t ) τ ( a ~ ) also occurs as the diagonal of some Hermitian matrix with the same set of eigenvalues, for any transposition τ in S n . One may prove that in the following manner.

Let ξ be a complex number of modulus 1 such that ξ a j k ¯ = − ξ a j k and U be a unitary matrix with ξ t , t in the j , j and k , k entries, respectively, − 1 − t 2 , ξ 1 − t 2 at the j , k and k , j entries, respectively, 1 at all diagonal entries other than j , j and k , k , and 0 at all other entries. Then U A U − 1 has t a j j + ( 1 − t ) a k k at the j , j entry, ( 1 − t ) a j j + t a k k at the k , k entry, and a l l at the l , l entry where l ≠ j , k . Let τ be the transposition of { 1 , 2 , … , n } that interchanges j and k .

Then the diagonal of U A U − 1 is t a ~ + ( 1 − t ) τ ( a ~ ) .

Λ is a Hermitian matrix with eigenvalues { λ i } i = 1 n . Using the equivalence of (i) and (iii) in the lemma mentioned above, we see that any vector in the permutation polytope generated by ( λ 1 , λ 2 , … , λ n ) , occurs as the diagonal of a Hermitian matrix with the prescribed eigenvalues. This proves Horn's theorem.

Symplectic geometry perspective

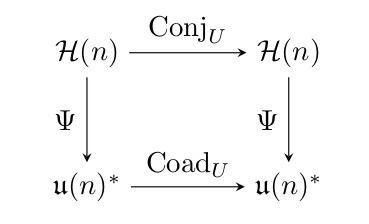
The Schur–Horn theorem may be viewed as a corollary of the Atiyah–Guillemin–Sternberg convexity theorem in the following manner. Let U ( n ) denote the group of n × n unitary matrices. Its Lie algebra, denoted by u ( n ) , is the set of skew-Hermitian matrices. One may identify the dual space u ( n ) ∗ with the set of Hermitian matrices H ( n ) via the linear isomorphism Ψ : H ( n ) → u ( n ) ∗ defined by Ψ ( A ) ( B ) = t r ( i A B ) for A ∈ H ( n ) , B ∈ u ( n ) . The unitary group U ( n ) acts on H ( n ) by conjugation and acts on u ( n ) ∗ by the coadjoint action. Under these actions, Ψ is an U ( n ) -equivariant map i.e. for every U ∈ U ( n ) the following diagram commutes,

Let λ ~ = ( λ 1 , λ 2 , … , λ n ) ∈ R n and Λ ∈ H ( n ) denote the diagonal matrix with entries given by λ ~ . Let O λ ~ denote the orbit of Λ under the U ( n ) -action i.e. conjugation. Under the U ( n ) -equivariant isomorphism Ψ , the symplectic structure on the corresponding coadjoint orbit may be brought onto O λ ~ . Thus O λ ~ is a Hamiltonian U ( n ) -manifold.

Let T denote the Cartan subgroup of U ( n ) which consists of diagonal complex matrices with diagonal entries of modulus 1 . The Lie algebra t of T consists of diagonal skew-Hermitian matrices and the dual space t ∗ consists of diagonal Hermitian matrices, under the isomorphism Ψ . In other words, t consists of diagonal matrices with purely imaginary entries and t ∗ consists of diagonal matrices with real entries. The inclusion map t ↪ u ( n ) induces a map Φ : H ( n ) ≅ u ( n ) ∗ → t ∗ , which projects a matrix A to the diagonal matrix with the same diagonal entries as A . The set O λ ~ is a Hamiltonian T -manifold, and the restriction of Φ to this set is a moment map for this action.

By the Atiyah–Guillemin–Sternberg theorem, Φ ( O λ ~ ) is a convex polytope. A matrix A ∈ H ( n ) is fixed under conjugation by every element of T if and only if A is diagonal. The only diagonal matrices in O λ ~ are the ones with diagonal entries λ 1 , λ 2 , … , λ n in some order. Thus, these matrices generate the convex polytope Φ ( O λ ~ ) . This is exactly the statement of the Schur–Horn theorem.