Scherrer equation

Applicability

The Scherrer equation is limited to nano-scale particles. It is not applicable to grains larger than about 0.1 to 0.2 μm, which precludes those observed in most metallographic and ceramographic microstructures.

It is important to realize that the Scherrer formula provides a lower bound on the particle size. The reason for this is that a variety of factors can contribute to the width of a diffraction peak besides instrumental effects and crystallite size; the most important of these are usually inhomogeneous strain and crystal lattice imperfections. The following sources of peak broadening are listed in reference: dislocations, stacking faults, twinning, microstresses, grain boundaries, sub-boundaries, coherency strain, chemical heterogeneities, and crystallite smallness. (Some of those and other imperfections may also result in peak shift, peak asymmetry, anisotropic peak broadening, or affect peak shape.)

If all of these other contributions to the peak width were zero, then the peak width would be determined solely by the crystallite size and the Scherrer formula would apply. If the other contributions to the width are non-zero, then the crystallite size can be larger than that predicted by the Scherrer formula, with the "extra" peak width coming from the other factors. The concept of crystallinity can be used to collectively describe the effect of crystal size and imperfections on peak broadening.

Derivation for a simple stack of planes

To see where the Scherrer equation comes from, it is useful to consider the simplest possible example:a set of N planes spaced a apart. The derivation for this simple, effectively one-dimensional case, is straightforward. First we will derive the structure factor for this case, and then determine an expression for the peak widths.

Structure factor for a set of N equally spaced planes

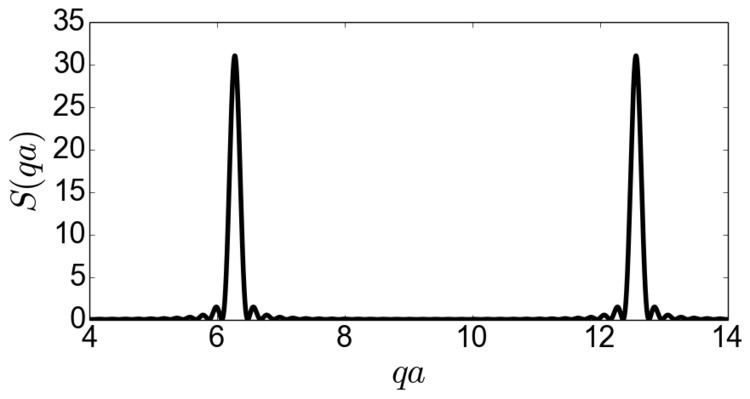
This system, effectively a one dimensional perfect crystal, has a structure factor or scattering function S(q)

S ( q ) = 1 N ∑ j , k = 1 N e − i q ( x j − x k )

where for N planes, x j = a j , so

S ( q ) = 1 N ∑ k = 1 N e − i q a k × ∑ j = 1 N e i q a j

the sums are simple geometric series, defining y = exp ⁡ ( i q a ) , ∑ j = 1 N = y j = ( y − y N + 1 ) / ( 1 − y ) , with the other series analogous. Then

S ( q ) = 1 N [ e − i q a − e − i q a ( N + 1 ) ] [ 1 − e − i q a ] × [ e i q a − e i q a ( N + 1 ) ] [ 1 − e i q a ]

S ( q ) = 1 N 2 − e i q a N − e − i q a N 2 − e i q a − e − i q a

converting to trigonometric functions

S ( q ) = 1 N 1 − cos ⁡ [ N q a ] 1 − cos ⁡ [ q a ]

and finally

S ( q ) = 1 N sin 2 ⁡ [ N q a / 2 ] sin 2 ⁡ [ q a / 2 ]

which gives a set of peaks at q P = 0 , 2 π / a , 4 π / a , … , all with heights S ( q P ) = N .

Determination of the profile near the peak, and hence the peak width

From the definition of FWHM, for a peak at q P and with a FWHM of Δ q , S ( q P ± Δ q ) = S ( q P ) / 2 = N / 2 , as the peak height is N. If we take the plus sign (peak is symmetric so either sign will do)

S ( q P + Δ q ) = 1 N sin 2 ⁡ [ N a ( q P + Δ q / 2 ) / 2 ] sin 2 ⁡ [ a ( q P + Δ q / 2 ) / 2 ] = N / 2

and

sin ⁡ [ N a ( q P + Δ q / 2 ) / 2 ] sin ⁡ [ a ( q P + Δ q / 2 ) / 2 ] = sin ⁡ [ N Δ q / 4 ] sin ⁡ [ Δ q a / 4 ] = N 2 1 / 2

as Δ q is small for not-too-small N, then sin ⁡ [ Δ q a / 2 ] ≃ Δ q a / 2 , and we can write the equation is a single non-linear equation sin ⁡ ( x ) − ( x / 2 1 / 2 ) = 0 , for x = N Δ q a / 4 . The solution to this equation is x = 1.39 . Therefore, the size of the set of planes is related to the FWHM in q by

τ = N a = 5.56 Δ q

To convert to an expression for crystal size in terms of the peak width in the scattering angle 2 θ used in X-ray powder diffraction, we note that the scattering vector q = ( 4 π / λ ) sin ⁡ ( θ ) . Then the peak width in the variable 2 θ is approximately β ≃ 2 Δ q / [ d q / d θ ] = 2 Δ q / [ ( 4 π / λ ) cos ⁡ ( θ ) ] , and so

τ = N a = 5.56 λ 2 π β cos ⁡ ( θ ) = 0.88 λ β cos ⁡ ( θ )

which is the Scherrer equation with K = 0.88.

This is all for 1D set of planes. In the experimentally relevant case of 3D, the form of S ( q ) and hence the peaks, depends on the crystal lattice type, and the size and shape of the nanocrystallite. The maths is also more involved than in this simple illustrative example. However, for simple lattices and shapes, expressions have been obtained for the FWHM, for example by Patterson. Just as in 1D, the FWHM varies as one oversize. For example, for a spherical particle with a cubic lattice, the factor of 5.56 simply becomes 6.96, when the size is the diameter D, i.e., the diameter of a spherical nanocrystal is related to the peak FWHM by

D = 6.96 Δ q or in θ : D = 1.11 λ β cos ⁡ ( θ )

Peak broadening due to disorder of the second kind

The finite size of a crystal is not the only possible reason for broadened peaks in X-ray diffraction. Fluctuations of atoms about the ideal lattice positions that preserve the long-range order of the lattice only give rise to the Debye-Waller factor, which reduces peak heights but does not broaden them. However, fluctuations that cause the correlations between nearby atoms to decrease as their separation increases, does broaden peaks. This can studied and quantified using the same simple one-dimensional stack of planes as above. The derivation follows that in chapter 9 of Guinier's textbook. This model has been pioneered by and applied to a number of materials bu Hosemann and collaborators over a number of years. They termed this disorder of the second kind, and referred to these imperfect crystalline ordering as paracrystalline ordering. Disorder of the first kind is the source of the Debye-Waller factor.

To derive the model we start with the definition of the structure factor

S ( q ) = 1 N ∑ j , k = 1 N e − i q ( x j − x k )

but now we want to consider, for simplicity an infinite crystal, i.e., N → ∞ , and we want to consider pairs of lattice sites. For large N , for each of these N planes, there are two neighbours m planes away, so the above double sum becomes a single sum over pairs of neighbours either side of an atom, at positions − m and m lattice spacings away, times N . So, then

S ( q ) = 1 + 2 N ∑ m = 1 N ∫ − ∞ ∞ d ( Δ x ) p m ( Δ x ) cos ⁡ ( m q Δ x )

where p m ( Δ x ) is the probability density function for the separation Δ x of a pair of planes, m lattice spacings apart. For the separation of neighbouring planes we assume for simplicity that the fluctuations around the mean neighbour spacing of a are Gaussian, i.e., that

p 1 ( Δ x ) = 1 ( 2 π σ 2 2 ) 1 / 2 exp ⁡ [ − ( Δ x − a ) 2 / ( 2 σ 2 2 ) ]

and we also assume that the fluctuations between a plane and its neighbour, and between this neighbour and the next plane, are independent. Then p 2 ( Δ x ) is just the convolution of two p 1 ( Δ x ) s, etc. As the convolution of two Gaussians is just another Gaussian, we have that

p m ( Δ x ) = 1 ( 2 π m σ 2 2 ) 1 / 2 exp ⁡ [ − ( Δ x − m a ) 2 / ( 2 m σ 2 2 ) ]

The sum in S ( q ) is then just a sum of Fourier Transforms of Gaussians, and so

S ( q ) = 1 + 2 ∑ m = 1 ∞ r m cos ⁡ ( m q a )

for r = exp ⁡ [ − q 2 σ 2 2 / 2 ] . The sum is just the real part of the sum ∑ m = 1 ∞ [ r exp ⁡ ( i q a ) ] m and so the structure factor of the infinite but disordered crystal is

S ( q ) = 1 − r 2 1 + r 2 − 2 r cos ⁡ ( q a )

This has peaks at maxima q p = 2 n π / a , where cos ⁡ ( q P a ) = 1 . These peaks have heights

S ( q P ) = 1 + r 1 − r ≈ 4 q P 2 σ 2 2 = 1 n 2 π 2 σ 2 2

i.e., the height of successive peaks drop off as the order of the peak (and so q ) squared. Unlike finite-size effects that broaden peaks but do not decrease their height, disorder lowers peak heights. Note that here we assuming that the disorder is relatively weak, so that we still have relatively well defined peaks. This is the limit q σ 2 ≪ 1 , where r ≃ 1 − q 2 σ 2 2 / 2 . In this limit, near a peak we can approximate cos ⁡ ( q a ) ≃ 1 − ( Δ q ) 2 a 2 / 2 , with Δ q = q − q P and obtain

S ( q ) ≈ S ( q P ) 1 + r ( 1 − r ) 2 Δ q 2 a 2 2 ≈ S ( q P ) 1 + Δ q 2 [ q P 2 σ 2 2 / a ] 2 / 2

which is a Lorentzian or Cauchy function, of FWHM q P 2 σ 2 2 / a = 4 π 2 n 2 ( σ 2 / a ) 2 / a , i.e., the FWHM increases as the square of the order of peak, and so as the square of the wavector q at the peak. Finally, the product of the peak height and the FWHM is constant and equals 4 / a , in the q σ 2 ≪ 1 limit. For the first few peaks where n is not large, this is just the σ 2 / a ≪ 1 limit.

Thus finite-size and this type of disorder both cause peak broadening, but there are qualitative differences. Finite-size effects broadens all peaks equally, and does not affect peak heights, while this type of disorder both reduces peak heights and broadens peaks by an amount that increases as n 2 . This, in principle, allows the two effects to be distinguished. Also, it means that the Scherrer equation is best applied to the first peak, as disorder of this type affects the first peak the least.

Coherence length

Within this model the degree of correlation between a pair of planes decreases as the distance between these planes increases, i.e., a pair of planes 10 planes apart have positions that are more weakly correlated than a pair of planes that are nearest neighbours. The correlation is given by p m , for a pair of planes m planes apart. For sufficiently large m the pair of planes are essentially uncorrelated, in the sense that the uncertainty in their relative positions is so large that it is comparable to the lattice spacing, a. This defines a correlation length, λ , defined as the separation when the width of p m , which is m 1 / 2 σ 2 equals a. This gives

λ = a 3 σ 2 2

which is in effect an order-of-magnitude estimate for the size of domains of coherent crystalline lattices. Note that the FWHM of the first peak scales as σ 2 2 / a 3 , so the coherence length is approximately 1/FWHM for the first peak.