Ruin theory

Classical model

The theoretical foundation of ruin theory, known as the Cramér–Lundberg model (or classical compound-Poisson risk model, classical risk process or Poisson risk process) was introduced in 1903 by the Swedish actuary Filip Lundberg. Lundberg's work was republished in the 1930s by Harald Cramér.

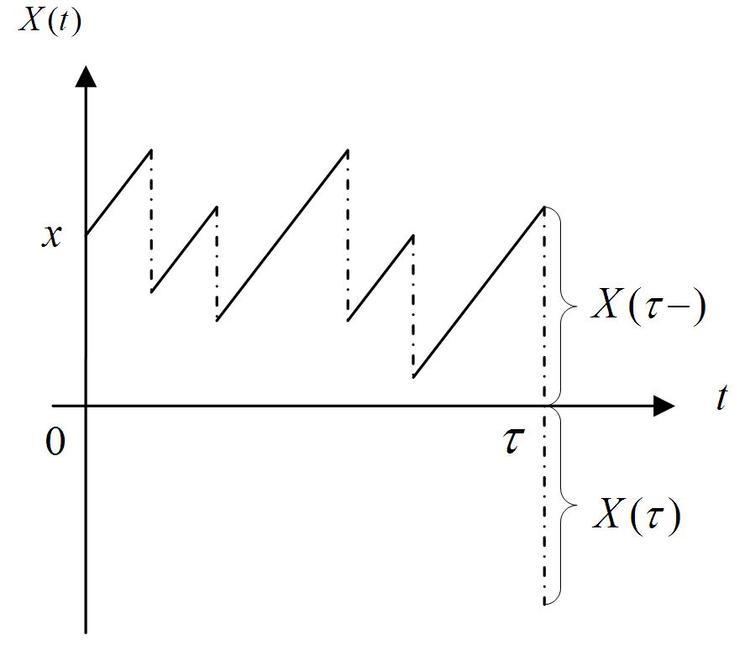
The model describes an insurance company who experiences two opposing cash flows: incoming cash premiums and outgoing claims. Premiums arrive a constant rate c > 0 from customers and claims arrive according to a Poisson process with intensity λ and are independent and identically distributed non-negative random variables with distribution F and mean μ (they form a compound Poisson process). So for an insurer who starts with initial surplus x,

The central object of the model is to investigate the probability that the insurer's surplus level eventually falls below zero (making the firm bankrupt). This quantity, called the probability of ultimate ruin, is defined as

where the time of ruin is τ = inf { t > 0 : X ( t ) < 0 } with the convention that inf ∅ = ∞ . This can be computed exactly using the Pollaczek–Khinchine formula as (the ruin function here is equivalent to the tail function of the stationary distribution of waiting time in an M/G/1 queue)

where F l ∗ n ( x ) is the transform of the tail distribution of F,

In the case where the claim sizes are exponentially distributed, this simplifies to

Sparre Andersen model

E. Sparre Andersen extended the classical model in 1957 by allowing claim inter-arrival times to have arbitrary distribution functions.

where the claim number process ( N t ) t ≥ 0 is a renewal process and ( ξ i ) i ∈ N are independent and identically distributed random variables. The model furthermore assumes that ξ i > 0 almost surely and that ( N t ) t ≥ 0 and ( ξ i ) i ∈ N are independent . The model is also known as the renewal risk model.

Expected discounted penalty function

Michael R. Powers and Gerber and Shiu analyzed the behavior of the insurer's surplus through the expected discounted penalty function, which is commonly referred to as Gerber-Shiu function in the ruin literature. It is arguable whether the function should have been called Powers-Gerber-Shiu function due to the contribution of Powers.

In Powers’ notation, this is defined as

where δ is the discounting force of interest, K τ is a general penalty function reflecting the economic costs to the insurer at the time of ruin, and the expectation E x corresponds to the probability measure P x . The function is called expected discounted cost of insolvency in Powers.

In Gerber and Shiu’s notation, it is given as

where δ is the discounting force of interest and w ( X τ − , X τ ) is a penalty function capturing the economic costs to the insurer at the time of ruin (assumed to depend on the surplus prior to ruin X τ − and the deficit at ruin X τ ), and the expectation E x corresponds to the probability measure P x . Here the indicator function I ( τ < ∞ ) emphasizes that the penalty is exercised only when ruin occurs.

It is quite intuitive to interpret the expected discounted penalty function. Since the function measures the actuarial present value of the penalty that occurs at τ , the penalty function is multiplied by the discounting factor e − δ τ , and then averaged over the probability distribution of the waiting time to τ . While Gerber and Shiu applied this function to the classical compound-Poisson model, Powers argued that an insurer’s surplus is better modeled by a family of diffusion processes.

There are a great variety of ruin-related quantities that fall into the category of the expected discounted penalty function.

Other finance-related quantities belonging to the class of the expected discounted penalty function include the perpetual American put option, the contingent claim at optimal exercise time, and more.

Recent developments