 | ||
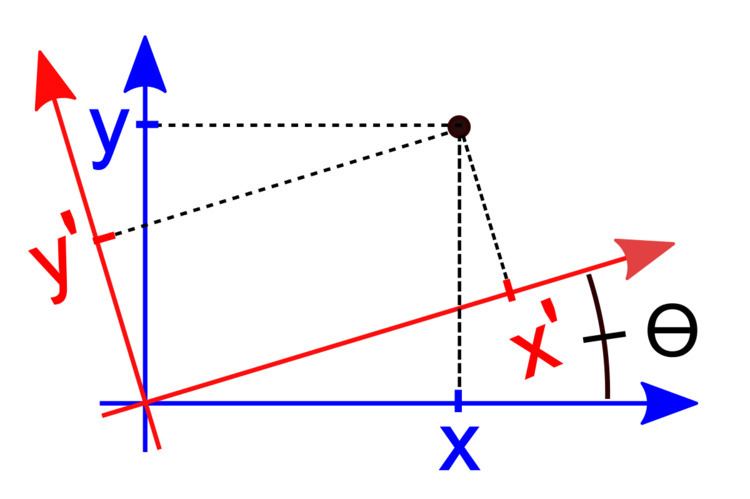
In mathematics, a rotation of axes in two dimensions is a mapping from an xy-Cartesian coordinate system to an x'y'-Cartesian coordinate system in which the origin is kept fixed and the x' and y' axes are obtained by rotating the x and y axes counterclockwise through an angle
Contents
Motivation
Coordinate systems are essential for studying the equations of curves using the methods of analytic geometry. To use the method of coordinate geometry, the axes are placed at a convenient position with respect to the curve under consideration. For example, to study the equations of ellipses and hyperbolas, the foci are usually located on one of the axes and are situated symmetrically with respect to the origin. If the curve (hyperbola, parabola, ellipse, etc.) is not situated conveniently with respect to the axes, the coordinate system should be changed to place the curve at a convenient and familiar location and orientation. The process of making this change is called a transformation of coordinates.
The solutions to many problems can be simplified by rotating the coordinate axes to obtain new axes through the same origin.
Derivation
The equations defining the transformation in two dimensions, which rotates the xy axes counterclockwise through an angle
In the xy system, let the point P have polar coordinates
We have
and
Substituting equations (1) and (2) into equations (3) and (4), we obtain
Equations (5) and (6) can be represented in matrix form as
which is the standard matrix equation of a rotation of axes in two dimensions.
The inverse transformation is
or
Example 1
Find the coordinates of the point
Solution:
The axes have been rotated counterclockwise through an angle of
Example 2
Find the coordinates of the point
Solution:
The axes have been rotated through an angle of
Rotation of conic sections
The most general equation of the second degree has the form
Through a change of coordinates (a rotation of axes and a translation of axes), equation (9) can be put into a standard form, which is usually easier to work with. It is always possible to rotate the coordinates in such a way that in the new system there is no x'y' term. Substituting equations (7) and (8) into equation (9), we obtain
where
If
When a problem arises with B, D and E all different from zero, they can be eliminated by performing in succession a rotation (eliminating B) and a translation (eliminating the D and E terms).
Identifying rotated conic sections
A non-degenerate conic section given by equation (9) can be identified by evaluating
Generalization to several dimensions
Suppose a rectangular xyz-coordinate system is rotated around its z axis counterclockwise (looking down the positive z axis) through an angle
Generalizing to any finite number of dimensions, a rotation matrix
for some
Example 3
Find the coordinates of the point
Solution:
