 | ||
In differential geometry, the Ricci flow (/ˈriːtʃi/, Italian: [ˈrittʃi]) is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric.
Contents
- Mathematical definition
- Einstein metrics
- Ricci solitons
- Relationship to uniformization and geometrization
- Relation to diffusion
- Recent developments
- References
The Ricci flow, named after Gregorio Ricci-Curbastro, was first introduced by Richard S. Hamilton in 1981 and is also referred to as the Ricci–Hamilton flow. It is the primary tool used in Grigori Perelman's solution of the Poincaré conjecture, as well as in the proof of the differentiable sphere theorem by Simon Brendle and Richard Schoen.
Mathematical definition
Given a Riemannian manifold with metric tensor
The normalized Ricci flow makes sense for compact manifolds and is given by the equation
where
The factor of −2 is of little significance, since it can be changed to any nonzero real number by rescaling t. However, the minus sign ensures that the Ricci flow is well defined for sufficiently small positive times; if the sign is changed, then the Ricci flow would usually only be defined for small negative times. (This is similar to the way in which the heat equation can be run forwards in time, but not usually backwards in time.)
Informally, the Ricci flow tends to expand negatively curved regions of the manifold, and contract positively curved regions.
Einstein metrics
Ricci solitons
Ricci solitons are Ricci flows that may change their size but not their shape up to diffeomorphisms.
Relationship to uniformization and geometrization
The Ricci flow was utilized by Richard S. Hamilton (1981) to gain insight into the geometrization conjecture of William Thurston, which concerns the topological classification of three-dimensional smooth manifolds. Hamilton's idea was to define a kind of nonlinear diffusion equation which would tend to smooth out irregularities in the metric. Then, by placing an arbitrary metric g on a given smooth manifold M and evolving the metric by the Ricci flow, the metric should approach a particularly nice metric, which might constitute a canonical form for M. Suitable canonical forms had already been identified by Thurston; the possibilities, called Thurston model geometries, include the three-sphere S3, three-dimensional Euclidean space E3, three-dimensional hyperbolic space H3, which are homogeneous and isotropic, and five slightly more exotic Riemannian manifolds, which are homogeneous but not isotropic. (This list is closely related to, but not identical with, the Bianchi classification of the three-dimensional real Lie algebras into nine classes.) Hamilton's idea was that these special metrics should behave like fixed points of the Ricci flow, and that if, for a given manifold, globally only one Thurston geometry was admissible, this might even act like an attractor under the flow.
Hamilton succeeded in proving that any smooth closed three-manifold which admits a metric of positive Ricci curvature also admits a unique Thurston geometry, namely a spherical metric, which does indeed act like an attracting fixed point under the Ricci flow, renormalized to preserve volume. (Under the unrenormalized Ricci flow, the manifold collapses to a point in finite time.) This doesn't prove the full geometrization conjecture, because the most difficult case turns out to concern manifolds with negative Ricci curvature and more specifically those with negative sectional curvature. (A strange and interesting fact is that all closed three-manifolds admit metrics with negative Ricci curvatures! This was proved by L. Zhiyong Gao and Shing-Tung Yau in 1986.)
Indeed, a triumph of nineteenth century geometry was the proof of the uniformization theorem, the analogous topological classification of smooth two-manifolds, where Hamilton showed that the Ricci flow does indeed evolve a negatively curved two-manifold into a two-dimensional multi-holed torus which is locally isometric to the hyperbolic plane. This topic is closely related to important topics in analysis, number theory, dynamical systems, mathematical physics, and even cosmology.
Note that the term "uniformization" suggests a kind of smoothing away of irregularities in the geometry, while the term "geometrization" suggests placing a geometry on a smooth manifold. Geometry is being used here in a precise manner akin to Klein's notion of geometry (see Geometrization conjecture for further details). In particular, the result of geometrization may be a geometry that is not isotropic. In most cases including the cases of constant curvature, the geometry is unique. An important theme in this area is the interplay between real and complex formulations. In particular, many discussions of uniformization speak of complex curves rather than real two-manifolds.
The Ricci flow does not preserve volume, so to be more careful, in applying the Ricci flow to uniformization and geometrization one needs to normalize the Ricci flow to obtain a flow which preserves volume. If one fails to do this, the problem is that (for example) instead of evolving a given three-dimensional manifold into one of Thurston's canonical forms, we might just shrink its size.
It is possible to construct a kind of moduli space of n-dimensional Riemannian manifolds, and then the Ricci flow really does give a geometric flow (in the intuitive sense of particles flowing along flowlines) in this moduli space.
Relation to diffusion
To see why the evolution equation defining the Ricci flow is indeed a kind of nonlinear diffusion equation, we can consider the special case of (real) two-manifolds in more detail. Any metric tensor on a two-manifold can be written with respect to an exponential isothermal coordinate chart in the form
(These coordinates provide an example of a conformal coordinate chart, because angles, but not distances, are correctly represented.)
The easiest way to compute the Ricci tensor and Laplace-Beltrami operator for our Riemannian two-manifold is to use the differential forms method of Élie Cartan. Take the coframe field
so that metric tensor becomes
Next, given an arbitrary smooth function
Take the Hodge dual
Take another exterior derivative
(where we used the anti-commutative property of the exterior product). That is,
Taking another Hodge dual gives
which gives the desired expression for the Laplace/Beltrami operator
To compute the curvature tensor, we take the exterior derivative of the covector fields making up our coframe:
From these expressions, we can read off the only independent Spin connection one-form
where we have taken advantage of the anti-symmetric property of the connection (
This gives the curvature two-form
from which we can read off the only linearly independent component of the Riemann tensor using
Namely
from which the only nonzero components of the Ricci tensor are
From this, we find components with respect to the coordinate cobasis, namely
But the metric tensor is also diagonal, with
and after some elementary manipulation, we obtain an elegant expression for the Ricci flow:
This is manifestly analogous to the best known of all diffusion equations, the heat equation
where now
The answer is that nonlinearity enters because the Laplace-Beltrami operator depends upon the same function p which we used to define the metric. But notice that the flat Euclidean plane is given by taking
Recent developments
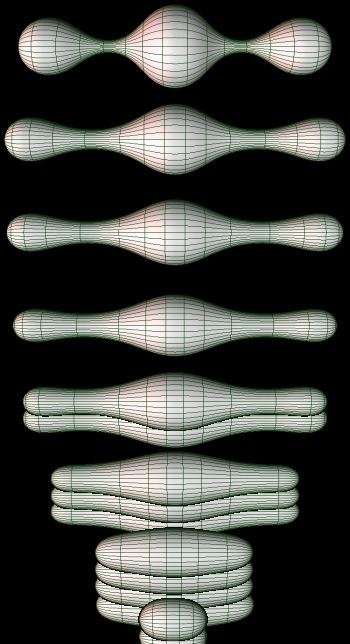
The Ricci flow has been intensively studied since 1981. Some recent work has focused on the question of precisely how higher-dimensional Riemannian manifolds evolve under the Ricci flow, and in particular, what types of parametric singularities may form. For instance, a certain class of solutions to the Ricci flow demonstrates that neckpinch singularities will form on an evolving n-dimensional metric Riemannian manifold having a certain topological property (positive Euler characteristic), as the flow approaches some characteristic time
For a 3-dimensional manifold, Perelman showed how to continue past the singularities using surgery on the manifold.
Kähler metrics remain Kähler under Ricci flow, and so Ricci flow has applications to the construction of Kähler–Einstein metrics.
