Relaxed intersection

Definition

The q-relaxed intersection of the m subsets X 1 , … , X m of R n , denoted by X { q } = ⋂ { q } X i is the set of all x ∈ R n which belong to all X i 's, except q at most. This definition is illustrated by Figure 1.

Define λ ( x ) = card { i   |   x ∈ X i } .

We have X { q } = λ − 1 ( [ m − q , m ] ) .

Characterizing the q-relaxed intersection is a thus a set inversion problem.

Example

Consider 8 intervals: X 1 = [ 1 , 4 ] , X 2 =   [ 2 , 4 ] , X 3 = [ 2 , 7 ] , X 4 = [ 6 , 9 ] , X 5 = [ 3 , 4 ] , X 6 = [ 3 , 7 ] .

We have

X { 0 } = ∅ , X { 1 } = [ 3 , 4 ] , X { 2 } = [ 3 , 4 ] , X { 3 } = [ 2 , 4 ] ∪ [ 6 , 7 ] , X { 4 } = [ 2 , 7 ] , X { 5 } = [ 1 , 9 ] , X { 6 } = ] − ∞ , ∞ [ .

Relaxed intersection of intervals

The relaxed intersection of intervals is not necessary an interval. We thus take the interval hull of the result. If X i 's are intervals, the relaxed intersection can be computed with a complexity of m.log(m) by using the Marzullo's algorithm. It suffices to sort all lower and upper bounds of the m intervals to represent the function λ . Then, we easily get the set

X { q } = λ − 1 ( [ m − q , m ] )

which corresponds to a union of intervals. We then return the smallest interval which contains this union.

Figure 2 shows the function λ ( x ) associated to the previous example.

Relaxed intersection of boxes

To compute the q-relaxed intersection of m boxes of R n , we project all m boxes with respect to the n axes. For each of the n groups of m intervals, we compute the q-relaxed intersection. We return Cartesian product of the n resulting intervals. Figure 3 provides an illustration of the 4-relaxed intersection of 6 boxes. Each point of the red box belongs to 4 of the 6 boxes.

Relaxed union

The q-relaxed union of X 1 , … , X m is defined by

⋃ { q } X i = ⋂ { m − 1 − q } X i

Note that when q=0, the relaxed union/intersection corresponds to the classical union/intersection. More precisely, we have

⋂ { 0 } X i = ⋂ X i

and

⋃ { 0 } X i = ⋃ X i

De Morgan's law

If X ¯ denotes the complementary set of X i , we have

⋂ { q } X i ¯ = ⋃ { q } X i ¯

⋃ { q } X i ¯ = ⋂ { q } X i ¯ .

As a consequence

⋂ { q } X i ¯ = ⋃ { m − q − 1 } X i ¯ = ⋂ { m − q − 1 } X i ¯

Relaxation of contractors

Let C 1 , … , C m be m contractors for the sets X 1 , … , X m , then

C ( [ x ] ) = ⋂ { q } C i ( [ x ] ) .

is a contractor for X { q } and

C ¯ ( [ x ] ) = ⋂ { m − q − 1 } C ¯ i ( [ x ] )

is a contractor for X ¯ { q } , where

C ¯ 1 , … , C ¯ m

are contractors for

X ¯ 1 , … , X ¯ m .

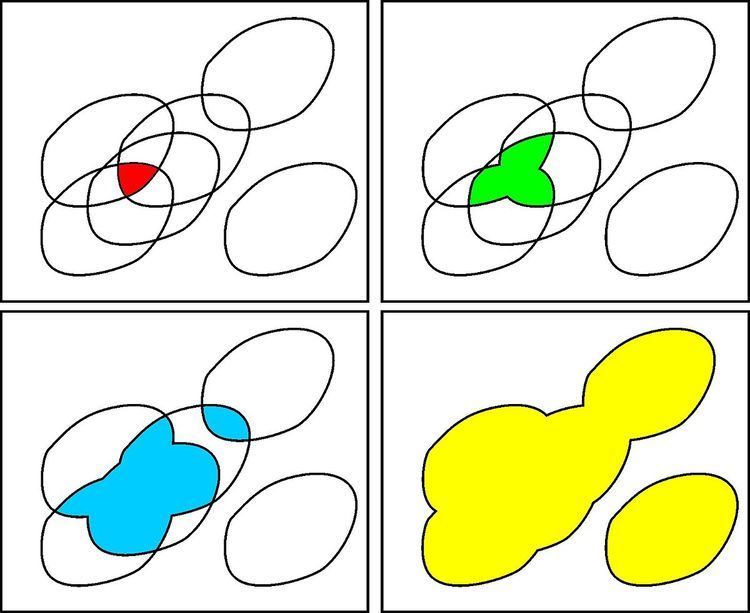
Combined with a branch-and-bound algorithm such as SIVIA (Set Inversion Via Interval Analysis), the q-relaxed intersection of m subsets of R n can be computed.

Application to bounded-error estimation

The q-relaxed intersection can be used for robust localization or for tracking.

Robust observers can also be implemented using the relaxed intersections to be robust with respect to outliers.

We propose here a simple example to illustrate the method. Consider a model the ith model output of which is given by

f i ( p ) = 1 2 π p 2 exp ⁡ ( − ( t i − p 1 ) 2 2 p 2 )

where p ∈ R 2 . Assume that we have

f i ( p ) ∈ [ y i ]

where t i and [ y i ] are given by the following list

{ ( 1 , [ 0 ; 0.2 ] ) , ( 2 , [ 0.3 ; 2 ] ) , ( 3 , [ 0.3 ; 2 ] ) , ( 4 , [ 0.1 ; 0.2 ] ) , ( 5 , [ 0.4 ; 2 ] ) , ( 6 , [ − 1 ; 0.1 ] ) }

The sets λ − 1 ( q ) for different q are depicted on Figure 4.