Puneet Varma (Editor)

Regular tree grammar

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Regular tree grammar

In theoretical computer science and formal language theory, a regular tree grammar (RTG) is a formal grammar that describes a set of directed trees, or terms. A regular word grammar can be seen as a special kind of regular tree grammar, describing a set of single-path trees.

Contents

Definition

A regular tree grammar G is defined by the tuple

G = (N, Σ, Z, P),

where

  • N is a finite set of nonterminals,
  • Σ is a ranked alphabet (i.e., an alphabet whose symbols have an associated arity) disjoint from N,
  • Z is the starting nonterminal, with Z ∈ N, and
  • P is a finite set of productions of the form A → t, with A ∈ N, and t ∈ TΣ(N), where TΣ(N) is the associated term algebra, i.e. the set of all trees composed from symbols in Σ ∪ N according to their arities, where nonterminals are considered nullary.

    • Derivation of trees

    The grammar G implicitly defines a set of trees: any tree that can be derived from Z using the rule set P is said to be described by G. This set of trees is known as the language of G. More formally, the relation ⇒G on the set TΣ(N) is defined as follows:

    A tree t1∈ TΣ(N) can be derived in a single step into a tree t2 ∈ TΣ(N) (in short: t1 ⇒G t2), if there is a context S and a production (A→t) ∈ P such that:

  • t1 = S[A], and
  • t2 = S[t].

    • Here, a context means a tree with exactly one hole in it; if S is such a context, S[t] denotes the result of filling the tree t into the hole of S.

    The tree language generated by G is the language L(G) = { t ∈ TΣ | Z ⇒G* t }.

    Here, TΣ denotes the set of all trees composed from symbols of Σ, while ⇒G* denotes successive applications of ⇒G.

    A language generated by some regular tree grammar is called a regular tree language.

    Examples

    Let G1 = (N1,Σ1,Z1,P1), where

  • N1 = {Bool, BList } is our set of nonterminals,
  • Σ1 = { true, false, nil, cons(.,.) } is our ranked alphabet, arities indicated by dummy arguments (i.e. the symbol cons has arity 2),
  • Z1 = BList is our starting nonterminal, and
  • the set P1 consists of the following productions:
  • Bool → false
  • Bool → true
  • BList → nil
  • BList → cons(Bool,BList)

    • An example derivation from the grammar G1 is

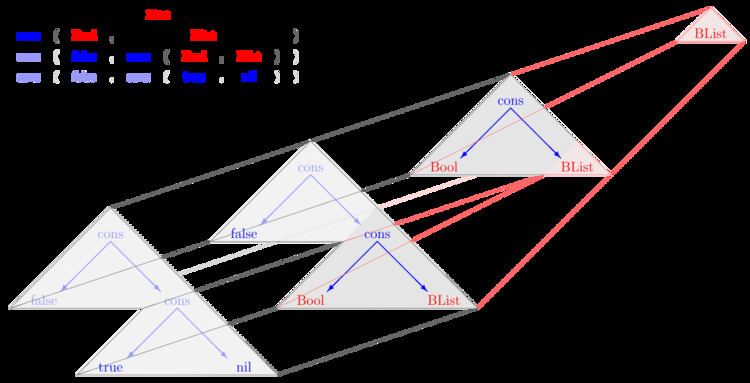
    BList ⇒ cons(Bool,BList) ⇒ cons(false,cons(Bool,BList)) ⇒ cons(false,cons(true,nil)).

    The image shows the corresponding derivation tree; it is a tree of trees (main picture), whereas a derivation tree in word grammars is a tree of strings (upper left table).

    The tree language generated by G1 is the set of all finite lists of boolean values, that is, L(G1) happens to equal TΣ1. The grammar G1 corresponds to the algebraic data type declarations (in the Standard ML programming language):

    Every member of L(G1) corresponds to a Standard-ML value of type BList.

    For another example, let G2 = (N1,Σ1,BList1,P1 ∪ P2), using the nonterminal set and the alphabet from above, but extending the production set by P2, consisting of the following productions:

  • BList1 → cons(true,BList)
  • BList1 → cons(false,BList1)

    • The language L(G2) is the set of all finite lists of boolean values that contain true at least once. The set L(G2) has no datatype counterpart in Standard ML, nor in any other functional language. It is a proper subset of L(G1). The above example term happens to be in L(G2), too, as the following derivation shows:

    BList1 ⇒ cons(false,BList1) ⇒ cons(false,cons(true,BList)) ⇒ cons(false,cons(true,nil)).

    Language properties

    If L1, L2 both are regular tree languages, then the tree sets L1 ∩ L2, L1 ∪ L2, and L1 \ L2 are also regular tree languages, and it is decidable whether L1 ⊆ L2, and whether L1 = L2.

    Alternative characterizations and relation to other formal languages

    Rajeev Alur and Parthasarathy Madhusudan related a subclass of regular binary tree languages to nested words and visibly pushdown languages.

    The regular tree languages are also the languages recognized by bottom-up tree automata and nondeterministic top-down tree automata.

    Regular tree grammars are a generalization of regular word grammars.

    Applications

    Applications of regular tree grammars include:

  • Instruction selection in compiler code generation
  • A decision procedure for the first-order logic theory of formulas over equality (=) and set membership (∈) as the only predicates
  • Solving constraints about mathematical sets
  • The set of all truths expressible in first-order logic about a finite algebra (which is always a regular tree language)

    • References

    Regular tree grammar Wikipedia
    (Text) CC BY-SA