 | ||
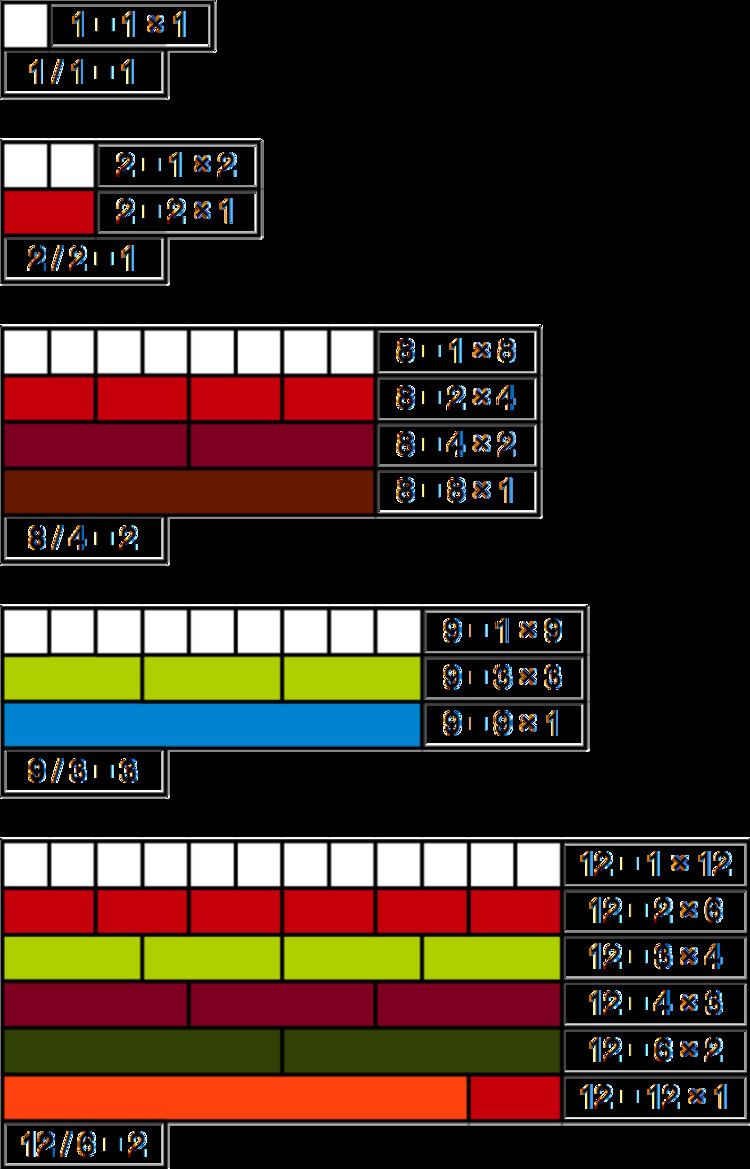
A refactorable number or tau number is an integer n that is divisible by the count of its divisors, or to put it algebraically, n is such that
Contents
1, 2, 8, 9, 12, 18, 24, 36, 40, 56, 60, 72, 80, 84, 88, 96, 104, 108, 128, 132, 136, 152, 156, 180, 184, 204, 225, 228, 232, 240, 248, 252, 276, 288, 296, ...For example, 18 has 6 divisors (1 and 18, 2 and 9, 3 and 6) and is divisible by 6.
Properties
Cooper and Kennedy proved that refactorable numbers have natural density zero. Zelinsky proved that no three consecutive integers can all be refactorable. Colton proved that no refactorable number is perfect. The equation GCD(n, x) = τ(n) has solutions only if n is a refactorable number.
There are still unsolved problems regarding refactorable numbers. Colton asked if there are there arbitrarily large n such that both n and n + 1 are refactorable. Zelinsky wondered if there exists a refactorable number
History
First defined by Curtis Cooper and Robert E. Kennedy where they showed that the tau numbers has natural density zero, they were later rediscovered by Simon Colton using a computer program he had made which invents and judges definitions from a variety of areas of mathematics such as number theory and graph theory. Colton called such numbers "refactorable". While computer programs had discovered proofs before, this discovery was one of the first times that a computer program had discovered a new or previously obscure idea. Colton proved many results about refactorable numbers, showing that there were infinitely many and proving a variety of congruence restrictions on their distribution. Colton was only later alerted that Kennedy and Cooper had previously investigated the topic.
