 | ||
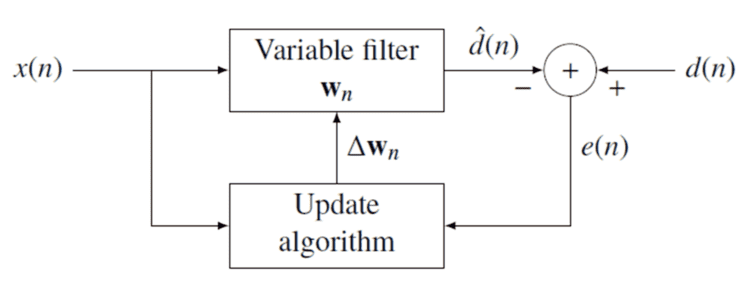
The Recursive least squares (RLS) is an adaptive filter which recursively finds the coefficients that minimize a weighted linear least squares cost function relating to the input signals. This is in contrast to other algorithms such as the least mean squares (LMS) that aim to reduce the mean square error. In the derivation of the RLS, the input signals are considered deterministic, while for the LMS and similar algorithm they are considered stochastic. Compared to most of its competitors, the RLS exhibits extremely fast convergence. However, this benefit comes at the cost of high computational complexity.
Contents
Motivation
RLS was discovered by Gauss but laid unused or ignored until 1950 when Plackett rediscovered the original work of Gauss from 1821. In general, the RLS can be used to solve any problem that can be solved by adaptive filters. For example, suppose that a signal d(n) is transmitted over an echoey, noisy channel that causes it to be received as
where
where
The benefit of the RLS algorithm is that there is no need to invert matrices, thereby saving computational power. Another advantage is that it provides intuition behind such results as the Kalman filter.
Discussion
The idea behind RLS filters is to minimize a cost function
The error implicitly depends on the filter coefficients through the estimate
The weighted least squares error function
where
The cost function is minimized by taking the partial derivatives for all entries
Next, replace
Rearranging the equation yields
This form can be expressed in terms of matrices
where
This is the main result of the discussion.
Choosing λ {\displaystyle \lambda }
The smaller
Recursive algorithm
The discussion resulted in a single equation to determine a coefficient vector which minimizes the cost function. In this section we want to derive a recursive solution of the form
where
where
Similarly we express
In order to generate the coefficient vector we are interested in the inverse of the deterministic auto-covariance matrix. For that task the Woodbury matrix identity comes in handy. With
The Woodbury matrix identity follows
To come in line with the standard literature, we define
where the gain vector
Before we move on, it is necessary to bring
Subtracting the second term on the left side yields
With the recursive definition of
Now we are ready to complete the recursion. As discussed
The second step follows from the recursive definition of
With
where
That means we found the correction factor
This intuitively satisfying result indicates that the correction factor is directly proportional to both the error and the gain vector, which controls how much sensitivity is desired, through the weighting factor,
RLS algorithm summary
The RLS algorithm for a p-th order RLS filter can be summarized as
Note that the recursion for
Lattice recursive least squares filter (LRLS)
The Lattice Recursive Least Squares adaptive filter is related to the standard RLS except that it requires fewer arithmetic operations (order N). It offers additional advantages over conventional LMS algorithms such as faster convergence rates, modular structure, and insensitivity to variations in eigenvalue spread of the input correlation matrix. The LRLS algorithm described is based on a posteriori errors and includes the normalized form. The derivation is similar to the standard RLS algorithm and is based on the definition of
Parameter Summary
LRLS Algorithm Summary
The algorithm for a LRLS filter can be summarized as
Normalized lattice recursive least squares filter (NLRLS)
The normalized form of the LRLS has fewer recursions and variables. It can be calculated by applying a normalization to the internal variables of the algorithm which will keep their magnitude bounded by one. This is generally not used in real-time applications because of the number of division and square-root operations which comes with a high computational load.
NLRLS algorithm summary
The algorithm for a NLRLS filter can be summarized as
