 | ||
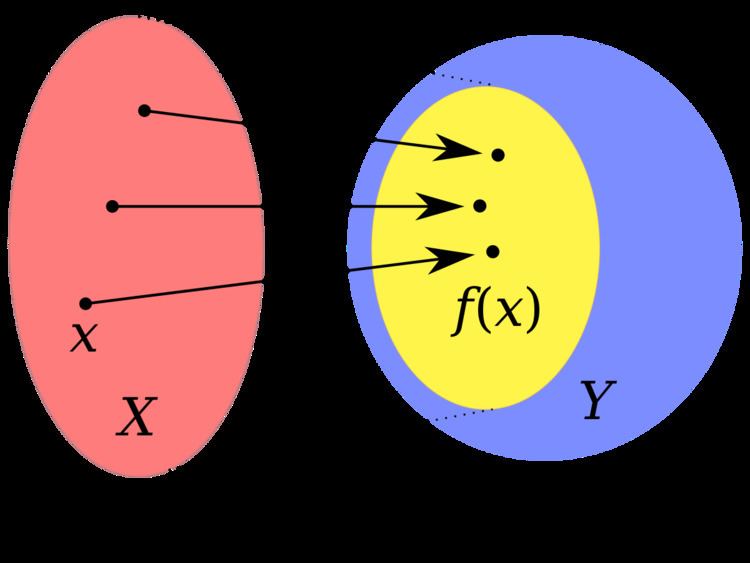
In mathematics, and more specifically in naive set theory, the range of a function refers to either the codomain or the image of the function, depending upon usage. Modern usage almost always uses range to mean image.
Contents
The codomain of a function is some arbitrary set. In real analysis, it is the real numbers. In complex analysis, it is the complex numbers.
The image of a function is the set of all outputs of the function. The image is always a subset of the codomain.
Distinguishing between the two uses
As the term "range" can have different meanings, it is considered a good practice to define it the first time it is used in a textbook or article.
Older books, when they use the word "range", tend to use it to mean what is now called the codomain. More modern books, if they use the word "range" at all, generally use it to mean what is now called the image. To avoid any confusion, a number of modern books don't use the word "range" at all.
As an example of the two different usages, consider the function
As an example where the range equals the codomain, consider the function
Formal definition
When "range" is used to mean "codomain", the image of a function f is already implicitely defined. It is (by definition of image) the (maybe trivial) subset of the "range" which equals {y | there exists an x in the domain of f such that y = f(x)}.
When "range" is used to mean "image", the range of a function f is by definition {y | there exists an x in the domain of f such that y = f(x)}. In this case, the codomain of f must not be specified, because any codomain with contains this image as a (maybe trivial) subset will work.
In both cases, image f ⊆ range f ⊆ codomain f, with at least one of the containments being equality.
