 | ||
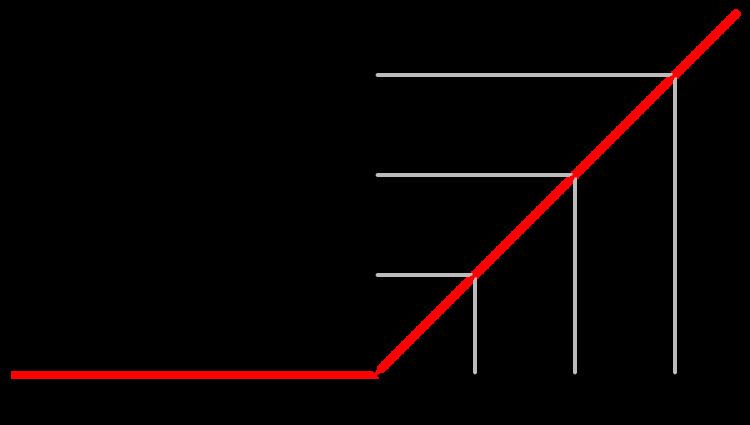
The ramp function is a unary real function, easily computable as the mean of the independent variable and its absolute value.
Contents
- Definitions
- Non negativity
- Derivative
- Second derivative
- Fourier transform
- Laplace transform
- Iteration invariance
- References
This function is applied in engineering (e.g., in the theory of DSP). The name ramp function is derived from the appearance of its graph.
Definitions
The ramp function (R(x) : ℝ → ℝ) may be defined analytically in several ways. Possible definitions are:
Non-negativity
In the whole domain the function is non-negative, so its absolute value is itself, i.e.
and
Derivative
Its derivative is the Heaviside function:
Second derivative
The ramp function satisfies the differential equation:
where δ(x) is the Dirac delta. This means that R(x) is a Green's function for the second derivative operator. Thus, any function, f(x), with an integrable second derivative, f″(x), will satisfy the equation:
Fourier transform
where δ(x) is the Dirac delta (in this formula, its derivative appears).
Laplace transform
The single-sided Laplace transform of R(x) is given as follows,
Iteration invariance
Every iterated function of the ramp mapping is itself, as
This applies the non-negative property.
