In graph theory, a path in an edge-colored graph is said to be rainbow if no color repeats on it. A graph is said to be rainbow-connected (or rainbow colored) if there is a rainbow path between each pair of its vertices. If there is a rainbow shortest path between each pair of vertices, the graph is said to be strongly rainbow-connected (or strongly rainbow colored).
Definitions and bounds
The rainbow connection number of a graph G is the minimum number of colors needed to rainbow-connect G , and is denoted by rc ( G ) . Similarly, the strong rainbow connection number of a graph G is the minimum number of colors needed to strongly rainbow-connect G , and is denoted by src ( G ) . Clearly, each strong rainbow coloring is also a rainbow coloring, while the converse is not true in general.
It is easy to observe that to rainbow-connect any connected graph G , we need at least diam ( G ) colors, where diam ( G ) is the diameter of G (i.e. the length of the longest shortest path). On the other hand, we can never use more than m colors, where m denotes the number of edges in G . Finally, because each strongly rainbow-connected graph is rainbow-connected, we have that diam ( G ) ≤ rc ( G ) ≤ src ( G ) ≤ m .
The following are the extremal cases:
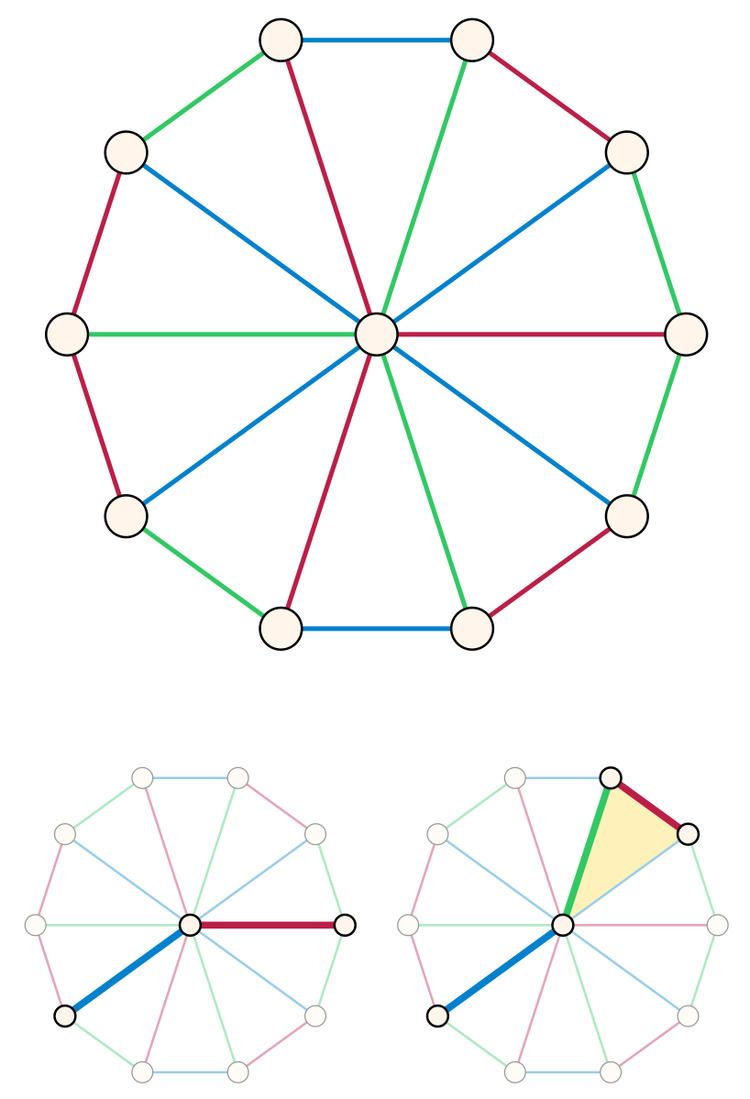
rc ( G ) = src ( G ) = 1 if and only if G is a complete graph. rc ( G ) = src ( G ) = m if and only if G is a tree.The above shows that in terms of the number of vertices, the upper bound rc ( G ) ≤ n − 1 is the best possible in general. In fact, a rainbow coloring using n − 1 colors can be constructed by coloring the edges of a spanning tree of G in distinct colors. The remaining uncolored edges are colored arbitrarily, without introducing new colors. When G is 2-connected, we have that rc ( G ) ≤ ⌈ n / 2 ⌉ . Moreover, this is tight as witnessed by e.g. odd cycles.
The rainbow or the strong rainbow connection number has been determined for some structured graph classes:
rc ( C n ) = src ( C n ) = ⌈ n / 2 ⌉ , for each integer n ≥ 4 , where C n is the cycle graph. rc ( W n ) = 3 , for each integer n ≥ 7 , and src ( W n ) = ⌈ n / 3 ⌉ , for n ≥ 3 , where W n is the wheel graph.The problem of deciding whether rc ( G ) = 2 for a given graph G is NP-complete. Because rc ( G ) = 2 if and only if src ( G ) = 2 , it follows that deciding if src ( G ) = 2 is NP-complete for a given graph G .
Variants and generalizations
Krivelevich and Yuster generalized the concept of rainbow connection to the vertex version. The rainbow vertex-connection number of a graph G is the minimum number of colors needed to color G such that for each pair of vertices, there is a path connecting them whose internal vertices are assigned distinct colors, and is denoted by rvc ( G ) .
Chartrand, Okamoto and Zhang generalized the rainbow connection number as follows. Let G be an edge-colored nontrivial connected graph of order n . A tree T is a rainbow tree if no two edges of T are assigned the same color. Let k be a fixed integer with 2 ≤ k ≤ n . An edge coloring of G is called a k -rainbow coloring if for every set S of k vertices of G , there is a rainbow tree in G containing the vertices of S . The k -rainbow index rx k ( G ) of G is the minimum number of colors needed in a k -rainbow coloring of G . A k -rainbow coloring using rx k ( G ) colors is called a minimum k -rainbow coloring. Thus rx 2 ( G ) is the rainbow connection number of G .