Quantum digital signature

Classical public-key method

The public-key method of cryptography allows a sender to sign a message (often only the cryptographic hash of the message) with a sign key in such a way that any recipient can, using the corresponding public key, check the authenticity of the message. To allow this, the public key is made broadly available to all potential recipients. To make sure only the legal author of the message can validly sign the message, the public key is created from a random, private sign key, using a one-way function. This is a function that is designed such that computing the result given the input is very easy, but computing the input given the result is very difficult. A classic example is the multiplication of two very large primes: The multiplication is easy, but factoring the product without knowing the primes is normally considered infeasible.

Quantum Digital Signature

Like classical digital signatures, quantum digital signatures make use of asymmetric keys. Thus, a person who wants to sign a message creates one or more pairs of sign and corresponding public keys. In general we can divide quantum digital signature schemes into two groups:

1. A scheme that creates a public quantum-bit key out of a private classical bit string: k ↦ | f k ⟩
2. A scheme that creates a public quantum-bit key out of a private quantum bit string: | k ⟩ ↦ | f k ⟩

In both cases f is a one-way quantum function that has the same properties as a classical one-way function. That is, the result is easy to compute, but, in contrast to the classical scheme, the function is impossible to invert, even if one uses powerful quantum cheating strategies.

The most famous scheme for the first method above is provided by Gottesman and Chuang

Requirements for a good and usable signature scheme

Most of the requirements for a classical digital signature scheme also apply to the quantum digital signature scheme.

In detail

1. The scheme has to provide security against tampering by
   1. The sender after the message was signed (see bit commitment)
   2. The receiver
   3. A third party
2. Creating a signed message has to be easy
3. Every recipient has to get the same answer, when testing the message for validity (Valid, Non-Valid)

Nature of the one-way function

A classical one-way function as said above is based on a classical infeasible mathematical task, whereas a quantum one-way function exploits the uncertainty principle which makes it impossible even for a quantum computer to compute the inverse. This is done by providing a quantum output state, with whom one cannot learn enough about the input string to reproduce it. In case of the first group of schemes this is shown by Holevo's theorem, which says, that from a given n-qubit quantum state one cannot extract more than n classical bits of information. One possibility to ensure that the scheme uses less qubits for a bit string of a certain length is by using nearly orthogonal states

That gives us the possibility to induce a basis with more than two states. So to describe an information of 2 n bits, we can use less than n qubits. An example with a 3 qubit basis

Only m qubits are needed to describe n classical bits when 3 m = 2 n holds.

Because of Holevo's theorem and the fact, that m can be much smaller than n, we can only get m bits out of the n bits message. More general, if one gets T copies of the public key he can extract at most Tm bits of the private key. If δ is big n − T m becomes very large, which makes it impossible for a dishonest person to guess the sign key.

Note: You cannot distinguish between non-orthogonal states, if you only have a small amount of identical states. That's how the quantum one-way functions works.
Nevertheless | f k ⟩ leaks information about the private key, in contrast to the classical public key, which forces one to get nothing or all about the private key.

Copying the public key

In the classical case we create a classical public key out of a classical sign key, thus it is easy to provide every potential recipient with a copy of the public key. The public key can be freely distributed. This becomes more difficult in the quantum case, because copying a quantum state is forbidden by the no cloning theorem, as long as the state itself is unknown. So public keys can only be created and distributed by a person who knows the exact quantum state he wants to create, thus who knows the sign key (This can be the sender or in more general a trustful institution). Nevertheless, in contrast to the classical public key there is an upper bound for the number of public quantum keys T which can be created, without enabling one to guess the sign key and thus endangering the security of the scheme ( n − T m has to be big)

Public Key should be the same for every recipient (Swap Test)

To make sure that every recipient gets identical results when testing the authenticity of a message, public keys distributed have to be the same. This is straightforward in the classical case, because one can easily compare two classical bit strings and see if those match. Nevertheless, in the quantum state it is more complicated. To test, if two public quantum states are the same one has to compare the following

This is done with the following quantum circuit which uses one Fredkin gate F, one Hadamard gate H and an ancilla qubit a. First of all the ancilla qubit is set to a symmetric state | a ⟩ = 1 2 ( | 0 ⟩ + | 1 ⟩ ) .

Right after the ancilla qubit is used as a control on the targets | f k ⟩   and   | f k ′ ⟩ in a Fredkin Gate.

Furthermore, a Hadamard gate is applied on the ancilla qubit and finally the first qubit gets measured. If both states are the same, the result | 0 ⟩ is measured. If both states are nearly orthogonal, the result can be either | 0 ⟩   or   | 1 ⟩ .

The calculation of the swap test in more detail:

The overall state

After the Fredkin gate is applied

⇒ 1 2 ( | 0 ⟩ | f k ⟩ | f k ′ ⟩ + | 1 ⟩ | f k ′ ⟩ | f k ⟩ )

After the Hadamard gate is applied on the first qubit

⇒ 1 2 [ ( | 0 ⟩ + | 1 ⟩ ) | f k ⟩ | f k ′ ⟩ + ( | 0 ⟩ − | 1 ⟩ ) | f k ′ ⟩ | f k ⟩ ]

After sorting for | 0 ⟩  and  | 1 ⟩

⇒ | ψ ⟩ = 1 2 [ | 0 ⟩ ( | f k ⟩ | f k ′ ⟩ + | f k ′ ⟩ | f k ⟩ ) + | 1 ⟩ ( | f k ⟩ | f k ′ ⟩ − | f k ′ ⟩ | f k ⟩ ) ]

Now it is easy to see, if the states | f k ⟩ = | f k ′ ⟩   then   | ψ ⟩ = | 0 ⟩ | f k ⟩ | f k ⟩ , which gives us a 0 whenever it is measured.

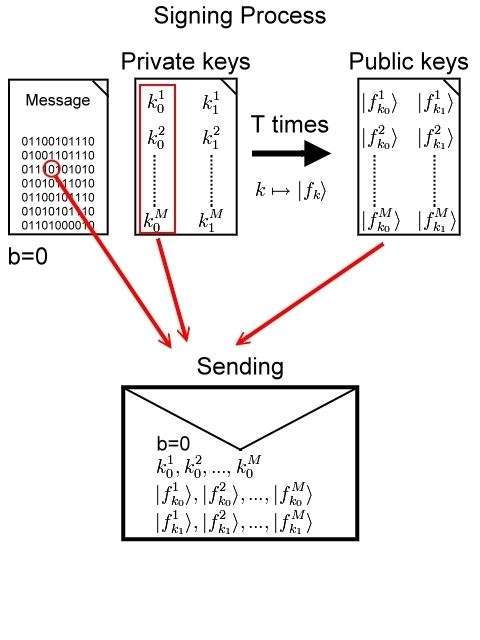
Signing Process

Let Person A (Alice) want to send a message to Person B (Bob). Hash algorithms won't be considered, so Alice has to sign every single bit of her message. Message-Bit b ∈ { 0 , 1 } .

Alice chooses M pairs of private keys { k 0 i , k 1 i } 1 ≤ i ≤ M

The function which maps k ↦ | f k ⟩ is known to all parties. Alice now computes the corresponding public keys { | f k 0 i ⟩ , | f k 1 i ⟩ } and gives all of them to the recipients. She can make as many copies as she needs, but has to take care, not to endanger the security ( n ≫ T m  has to hold  ) .

Her level of security limits the number of identical public keys she can create

If

Remember: In this example Alice picks only one bit b and signs it. She has to do that for every single bit in her message

Validation Process

Bob now possesses

Now Bob calculates | f k b ⟩ for all received private keys (either k 0  or  k 1 ).

After he has done so he makes use of the swap test to compare the calculated states with the received public keys. Since the swap test has some probability to give the wrong answer he has to do it for all the M keys and counts how many incorrect keys he gets r. It is obvious, that M is some kind of a security parameter. It is more unlikely to validate a bit wrong for bigger M.

Avoid a message to be validated differently

One problem which arises especially for small M is, that the number of incorrect keys different recipients measure differ with probability. So to define only one threshold is not enough, because it would cause a message to be validated differently, when the number of incorrect keys r is very close to the defined threshold.

This can be prevented by defining more than one threshold. Because the number of errors increase proportional with M, the thresholds are defined like

If we assume perfect channels without noise, so the bit can't be changed due to the transfer, then the threshold T a can be set to zero, because the swap test passes always, when the compared states are the same