 | ||
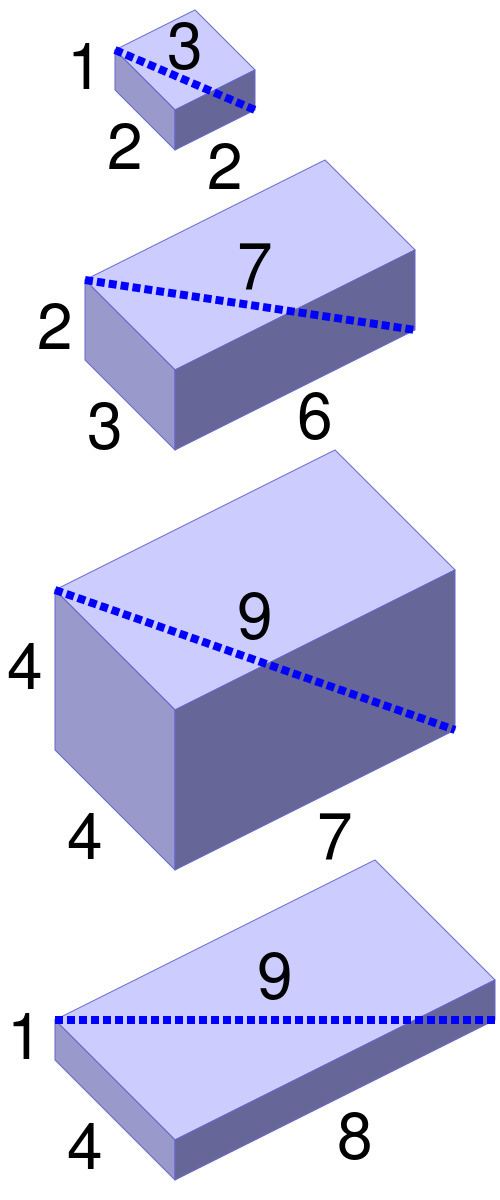
A Pythagorean quadruple is a tuple of integers a, b, c and d, such that d > 0 and a2 + b2 + c2 = d2. Geometrically, a Pythagorean quadruple (a, b, c, d) defines a cuboid with integer side lengths | a |, | b |, and | c |, whose space diagonal has integer length d. Pythagorean quadruples are thus also called Pythagorean boxes.
Contents
Parametrization of primitive quadruples
A Pythagorean quadruple is called primitive if the greatest common divisor of its entries is 1. Every Pythagorean quadruple is an integer multiple of a primitive quadruple. The set of primitive Pythagorean quadruples for which a is odd is parametrized by
where m, n, p, q are non-negative integers with greatest common divisor 1 such that m + n + p + q is odd. Thus, all primitive Pythagorean quadruples are characterized by the Lebesgue identity
Alternate parametrization
All Pythagorean quadruples (including non-primitives, and with repetition, though a, b and c do not appear in all possible orders) can be generated from two positive integers a and b as follows:
If a and b have different parity, let p be any factor of a2 + b2 such that p2 < a2 + b2. Then c = a2 + b2 − p2/2p and d = a2 + b2 + p2/2p. Note that p = d − c.
A similar method exists for generating all Pythagorean quadruples for which a and b are both even. Let l = a/2 and m = b/2 and let n be a factor of l2 + m2 such that n2 < l2 + m2. Then c = l2 + m2 − n2/n and d = l2 + m2 + n2/n. This method generates all Pythagorean quadruples exactly once each when l and m run through all pairs of natural numbers and n runs through all permissible values for each pair.
No such method exists if both a and b are odd, in which case no solutions exist as can be seen by the parametrization in the previous section.
Properties
The largest number that always divides the product abcd is 12. The quadruple with the minimal product is (1, 2, 2, 3).
Relationship with quaternions and rational orthogonal matrices
A primitive Pythagorean quadruple (a, b, c, d) parametrized by (m,n,p,q) corresponds to the first column of the matrix representation E(α) of conjugation α(⋅)α by the Hurwitz quaternion α = m + ni + pj + qk restricted to the subspace of ℍ spanned by i, j, k, which is given by
where the columns are pairwise orthogonal and each has norm d. Furthermore, we have 1/dE(α) ∈ SO(3,ℚ), and, in fact, all 3 × 3 orthogonal matrices with rational coefficients arise in this manner.
Primitive Pythagorean quadruples with small norm
There are 31 primitive Pythagorean quadruples in which all entries are less than 30.
