Pseudo arc

History

In 1920, Bronisław Knaster and Kazimierz Kuratowski asked whether a nondegenerate homogeneous continuum in the Euclidean plane R² must be a Jordan curve. In 1921, Stefan Mazurkiewicz asked whether a nondegenerate continuum in R² that is homeomorphic to each of its nondegenerate subcontinua must be an arc. In 1922, Knaster discovered the first example of a homogeneous hereditarily indecomposable continuum K, later named the pseudo-arc, giving a negative answer to the Mazurkiewicz question. In 1948, R.H. Bing proved that Knaster's continuum is homogeneous, i.e. for any two of its points there is a homeomorphism taking one to the other. Yet also in 1948, Edwin Moise showed that Knaster's continuum is homeomorphic to each of its non-degenerate subcontinua. Due to its resemblance to the fundamental property of the arc, namely, being homeomorphic to all its nondegenerate subcontinua, Moise called his example M a pseudo-arc. Bing's construction is a modification of Moise's construction of M, which he had first heard described in a lecture. In 1951, Bing proved that all hereditarily indecomposable arc-like continua are homeomorphic — this implies that Knaster's K, Moise's M, and Bing's B are all homeomorphic. Bing also proved that the pseudo-arc is typical among the continua in a Euclidean space of dimension at least 2 or an infinite-dimensional separable Hilbert space.

Construction

The following construction of the pseudo-arc follows (Wayne Lewis 1999).

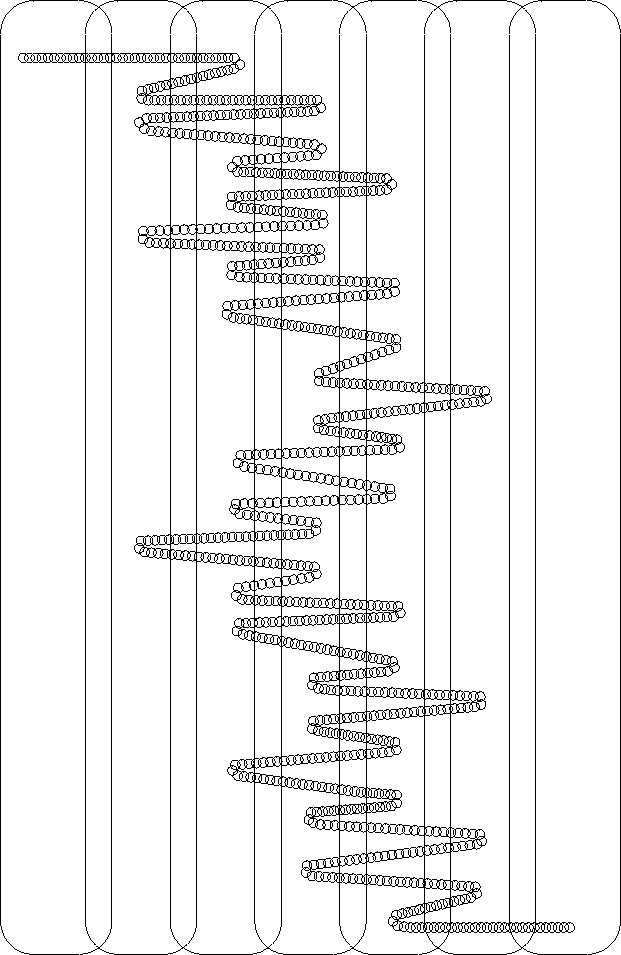
Chains

At the heart of the definition of the pseudo-arc is the concept of a chain, which is defined as follows:

A chain is a finite collection of open sets C = { C 1 , C 2 , … , C n } in a metric space such that C i ∩ C j ≠ ∅ if and only if | i − j | ≤ 1. The elements of a chain are called its links, and a chain is called an ε-chain if each of its links has diameter less than ε.

While being the simplest of the type of spaces listed above, the pseudo-arc is actually very complex. The concept of a chain being crooked (defined below) is what endows the pseudo-arc with its complexity. Informally, it requires a chain to follow a certain recursive zig-zag pattern in another chain. To 'move' from the mth link of the larger chain to the nth, the smaller chain must first move in a crooked manner from the mth link to the (n-1)th link, then in a crooked manner to the (m+1)th link, and then finally to the nth link.

More formally:

Let C and D be chains such that

1. each link of D is a subset of a link of C , and
2. for any indices i, j, m, and n with D i ∩ C m ≠ ∅ , D j ∩ C n ≠ ∅ , and m < n − 2 , there exist indices k and ℓ with i < k < ℓ < j (or i > k > ℓ > j ) and D k ⊆ C n − 1 and D ℓ ⊆ C m + 1 .

Then D is crooked in C .

Pseudo-arc

For any collection C of sets, let C ∗ denote the union of all of the elements of C. That is, let

C ∗ = ⋃ S ∈ C S .

The pseudo-arc is defined as follows:

Let p and q be distinct points in the plane and { C i } i ∈ N be a sequence of chains in the plane such that for each i,

1. the first link of C i contains p and the last link contains q,
2. the chain C i is a 1 / 2 i -chain,
3. the closure of each link of C i + 1 is a subset of some link of C i , and
4. the chain C i + 1 is crooked in C i .

Let Then P is a pseudo-arc.