Prüfer sequence

Algorithm to convert a tree into a Prüfer sequence

One can generate a labeled tree's Prüfer sequence by iteratively removing vertices from the tree until only two vertices remain. Specifically, consider a labeled tree T with vertices {1, 2, ..., n}. At step i, remove the leaf with the smallest label and set the ith element of the Prüfer sequence to be the label of this leaf's neighbour.

The Prüfer sequence of a labeled tree is unique and has length n − 2.

Example

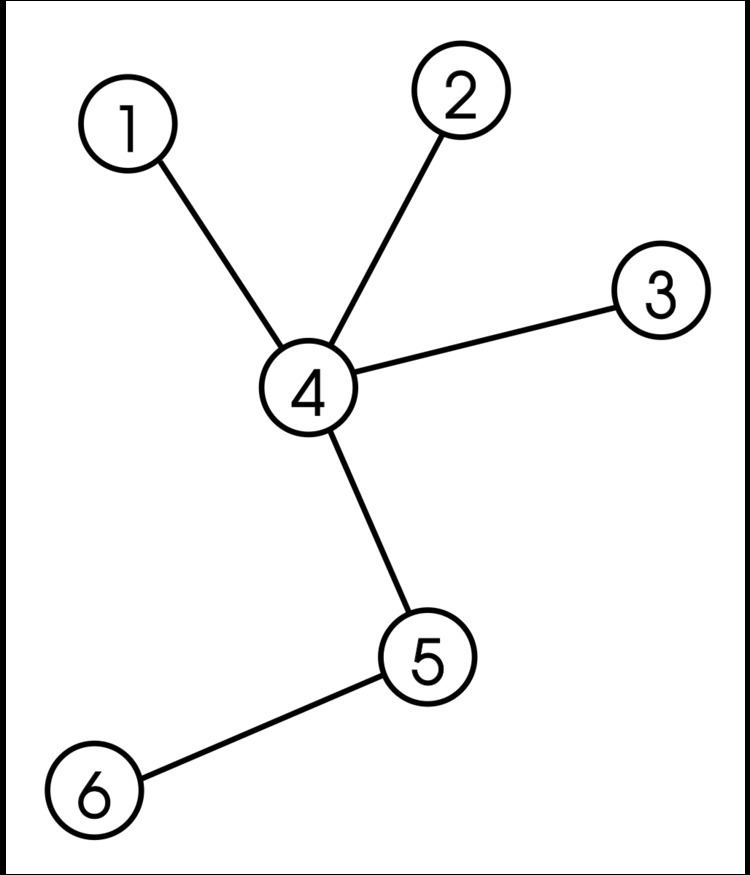
Consider the above algorithm run on the tree shown to the right. Initially, vertex 1 is the leaf with the smallest label, so it is removed first and 4 is put in the Prüfer sequence. Vertices 2 and 3 are removed next, so 4 is added twice more. Vertex 4 is now a leaf and has the smallest label, so it is removed and we append 5 to the sequence. We are left with only two vertices, so we stop. The tree's sequence is {4,4,4,5}.

Algorithm to convert a Prüfer sequence into a tree

Let {a[1], a[2], ..., a[n]} be a Prüfer sequence:

The tree will have n+2 nodes, numbered from 1 to n+2. For each node set its degree to the number of times it appears in the sequence plus 1. For instance, in pseudo-code:

Convert-Prüfer-to-Tree(a) 1 n ← length[a] 2 T ← a graph with n + 2 isolated nodes, numbered 1 to n + 2 3 degree ← an array of integers 4 for each node i in T 5 do degree[i] ← 1 6 for each value i in a 7 do degree[i] ← degree[i] + 1

Next, for each number in the sequence a[i], find the first (lowest-numbered) node, j, with degree equal to 1, add the edge (j, a[i]) to the tree, and decrement the degrees of j and a[i]. In pseudo-code:

8 for each value i in a 9 for each node j in T10 if degree[j] = 111 then Insert edge[i, j] into T12 degree[i] ← degree[i] - 113 degree[j] ← degree[j] - 114 break

At the end of this loop two nodes with degree 1 will remain (call them u, v). Lastly, add the edge (u,v) to the tree.

15 u ← v ← 016 for each node i in T17 if degree[i] = 118 then if u = 019 then u ← i20 else v ← i21 break22 Insert edge[u, v] into T23 degree[u] ← degree[u] - 124 degree[v] ← degree[v] - 125 return T

Cayley's formula

The Prüfer sequence of a labeled tree on n vertices is a unique sequence of length n − 2 on the labels 1 to n — this much is clear. Somewhat less obvious is the fact that for a given sequence S of length n–2 on the labels 1 to n, there is a unique labeled tree whose Prüfer sequence is S.

The immediate consequence is that Prüfer sequences provide a bijection between the set of labeled trees on n vertices and the set of sequences of length n–2 on the labels 1 to n. The latter set has size nⁿ⁻², so the existence of this bijection proves Cayley's formula, i.e. that there are nⁿ⁻² labeled trees on n vertices.

Other applications

Cayley's formula can be strengthened to prove the following claim:

The number of spanning trees in a complete graph K n with a degree d i specified for each vertex i is equal to the multinomial coefficient ( n − 2 d 1 − 1 , d 2 − 1 , … , d n − 1 ) = ( n − 2 ) ! ( d 1 − 1 ) ! ( d 2 − 1 ) ! ⋯ ( d n − 1 ) ! . The proof follows by observing that in the Prüfer sequence number i appears exactly ( d i − 1 ) times.

Cayley's formula can be generalized: a labeled tree is in fact a spanning tree of the labeled complete graph. By placing restrictions on the enumerated Prüfer sequences, similar methods can give the number of spanning trees of a complete bipartite graph. If G is the complete bipartite graph with vertices 1 to n₁ in one partition and vertices n₁ + 1 to n in the other partition, the number of labeled spanning trees of G is n 1 n 2 − 1 n 2 n 1 − 1 , where n₂ = n − n₁.

Generating uniformly distributed random Prüfer sequences and converting them into the corresponding trees is a straightforward method of generating uniformly distributed random labelled trees.