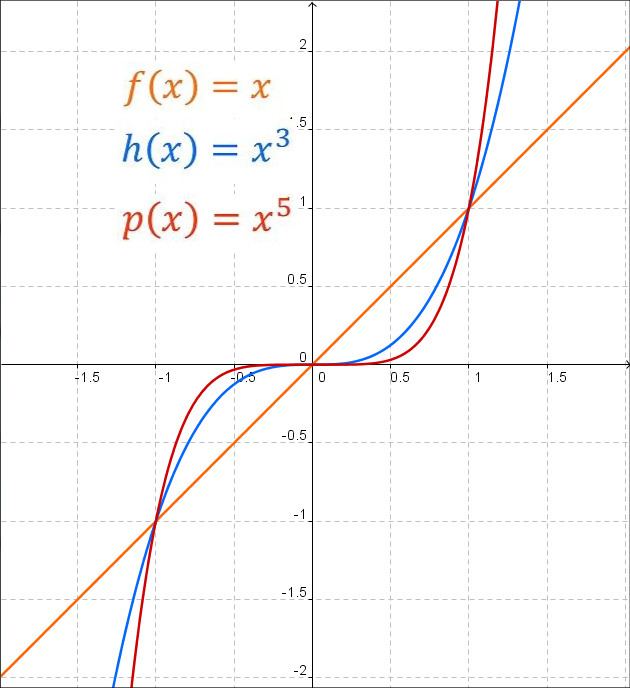In mathematics, a power function is a function of the form
f
(
x
)
=
x
p
where
p
is constant and
x
is a variable. In general,
p
can belong to one of several classes of numbers, such as the positive and negative integers. They are a fundamental concept in algebra and pre-calculus, leading up to the formation of polynomials. Their general form is
f
(
x
)
=
c
x
p
, where
c
is also a constant.
When
c
=
0
,
f
(
x
)
is the constant function
f
(
x
)
=
0
for all real
x
. Graphically, it is a horizontal line at
y
=
0
, and can be thought of as the function that maps all inputs to 0, the number zero.
When
p
=
0
,
f
(
x
)
is the constant function
f
(
x
)
=
1
for all real
x
. Graphically, it is a horizontal line at
y
=
1
, and can be thought of similarly to the previous case; it simply maps all inputs to 1, the number one.
When
p
=
1
,
f
(
x
)
is the identity function
f
(
x
)
=
x
. Graphically, it is a line through the origin with slope 1, and can be thought of as the function that maps every input to itself.
When
p
is in
Z
and
p
≥
2
, two primary families exist: when
p
is even, and when
p
is odd. In general, when
p
is even and
x
is large,
f
(
x
)
will tend towards positive infinity if
c
≥
0
, and toward negative infinity if
c
≤
0
. All even power function graphs of this family have the general shape of
y
=
x
2
, flattening more in the middle as
p
increases. Functions with this kind of symmetry are called even functions.
When
p
is odd,
f
(
x
)
's asymptotic behavior reverses from positive
x
to negative
x
. For
c
≥
0
, and large and positive
x
,
f
(
x
)
will tend towards positive infinity, while for large and negative
x
,
f
(
x
)
will tend towards negative infinity. For
c
≤
0
, the opposite is true in each case. All odd power function graphs of this family have the general shape of
y
=
x
3
, flattening more in the middle as
p
increases. Functions with this kind of symmetry are called odd functions.
When
p
is in
Z
and
p
<
0
,
f
(
x
)
takes the shape of a hyperbola. As with positive integers, there exist two primary families according to
p
's parity. Regardless of said parity, however, these families all tend toward zero for large
x
, whether positive or negative. Where their behavior differs is in approaching
x
=
0
from the right and left.
When
p
is even,
f
(
x
)
is even, and thus symmetric about the
y
-axis. Thus, when approaching
x
=
0
from either the right or the left,
f
(
x
)
will tend towards positive infinity when
c
is positive, and negative infinity when
c
is negative.
When
p
is odd,
f
(
x
)
is odd, and thus symmetric about the origin.
Polynomials, another fundamental algebraic construct, can be seen as being created from multiple power functions and their coefficient terms (i.e.
c
x
n
), added together. For example,
f
(
x
)
=
x
2
+
2
x
+
1
or
f
(
x
)
=
x
+
x
3
.
Power functions are a special case of power law relationships, which appear throughout mathematics and statistics.