Polyhedral skeletal electron pair theory

Predicting structures of cluster compounds

Different rules (4n, 5n, or 6n) are invoked depending on the number of electrons per vertex.

The 4n rules are reasonably accurate in predicting the structures of clusters having about 4 electrons per vertex, as is the case for many boranes and carboranes. For such clusters, the structures are based on deltahedra, which are polyhedra in which every face is triangular. The 4n clusters are classified as closo-, nido-, arachno- or hypho-, based on whether they represent a complete (closo-) deltahedron, or a deltahedron that is missing one (nido-), two (arachno-) or three (hypho-) vertices.

However, hypho clusters are relatively uncommon due to the fact that the electron count is high enough to start to fill antibonding orbitals and destabilize the 4n structure. If the electron count is close to 5 electrons per vertex, the structure often changes to one governed by the 5n rules, which are based on 3-connected polyhedra.

As the electron count increases further, the structures of clusters with 5n electron counts become unstable, so the 6n rules can be implemented. The 6n clusters have structures that are based on rings.

A molecular orbital treatment can be used to rationalize the bonding of cluster compounds of the 4n, 5n, and 6n types.

4n rules

The following polyhedra are closo polyhedra, and are the basis for the 4n rules; each of these have triangular faces. The number of vertices in the cluster determines what polyhedron the structure is based on.

Using the electron count, the predicted structure can be found. n is the number of vertices in the cluster. The 4n rules are enumerated in the following table.

When counting electrons for each cluster, the number of valence electrons is enumerated. For each transition metal present, 10 electrons are subtracted from the total electron count. For example, in Rh₆(CO)₁₆ the total number of electrons would be 6 × 9 + 16 × 2 − 6 × 10 = 86 – 6 × 10 = 26. Therefore, the cluster is a closo polyhedron because n = 6, with 4n + 2 = 26.

Other rules may be considered when predicting the structure of clusters:

1. For clusters consisting mostly of transition metals, any main group elements present are often best counted as ligands or interstitial atoms, rather than vertices.
2. Larger and more electropositive atoms tend to occupy vertices of high connectivity and smaller more electronegative atoms tend to occupy vertices of low connectivity.
3. In the special case of boron hydride clusters, each boron connected to 3 or more vertices has one terminal hydride, while a boron connected to 2 other vertices has 2 terminal hydrogens. If more hydrogens are present, they are placed in open face positions to even out the coordination number of the vertices.
4. For the special case of transition metal clusters, ligands are added to the metal centers to give the metals reasonable coordination numbers, and if any hydrogen atoms are present they are placed in bridging positions to even out the coordination numbers of the vertices.

In general, closo structures with n vertices are n-vertex polyhedra.

To predict the structure of a nido cluster, the closo cluster with n + 1 vertices is used as a starting point; if the cluster is composed of small atoms a high connectivity vertex is removed, while if the cluster is composed of large atoms a low connectivity vertex is removed.

To predict the structure of an arachno cluster, the closo polyhedron with n + 2 vertices is used as the starting point, and the n + 1 vertex nido complex is generated by following the rule above; a second vertex adjacent to the first is removed if the cluster is composed of mostly small atoms, a second vertex not adjacent to the first is removed if the cluster is composed mostly of large atoms.

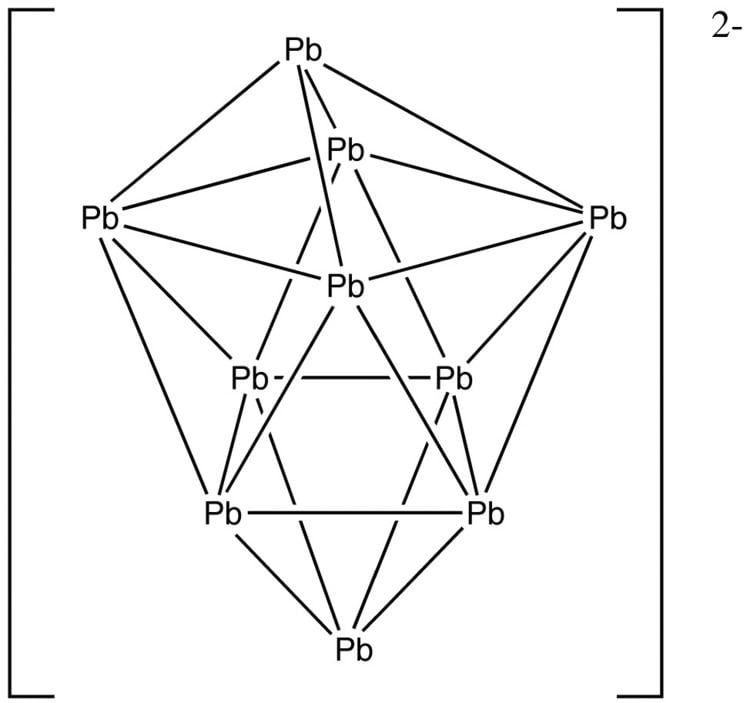
Example: Pb2−
10

Electron count: 10 × Pb + 2 (for the negative charge) = 10 × 4 + 2 = 42 electrons. Since n = 10, 4n + 2 = 42, so the cluster is a closo bicapped square antiprism.

Example: S2+
4

Electron count: 4 × S – 2 (for the positive charge) = 4 × 6 – 2 = 22 electrons. Since n = 4, 4n + 6 = 22, so the cluster is arachno. Starting from an octahedron, a vertex of high connectivity is removed, and then a non-adjacent vertex is removed.

Example: Os₆(CO)₁₈

Electron count: 6 × Os + 18 × CO – 60 (for 6 osmium atoms) = 6 × 8 + 18 × 2 – 60 = 24 Since n = 6, 4n = 24, so the cluster is capped closo. Starting from a trigonal bipyramid, a face is capped. The carbonyls have been omitted for clarity.

Example: B
5H4−
5

Electron count: 5 × B + 5 × H + 4 (for the negative charge) = 5 × 3 + 5 × 1 + 4 = 24 Since n = 5, 4n + 4 = 24, so the cluster is nido. Starting from an octahedron, one of the vertices is removed.

The rules are useful in also predicting the structure of carboranes. Example: C₂B₇H₁₃

Electron count = 2 × C + 7 × B + 13 × H = 2 × 4 + 3 × 7 + 13 × 1 = 42 Since n in this case is 9, 4n + 6 = 42, the cluster is arachno.

The bookkeeping for deltahedral clusters is sometimes carried out by counting skeletal electrons instead of the total number of electrons. The skeletal orbital (electron pair) and skeletal electron counts for the four types of deltahedral clusters are:

n-vertex closo: n + 1 skeletal orbitals, 2n + 2 skeletal electrons

n-vertex nido: n + 2 skeletal orbitals, 2n + 4 skeletal electrons

n-vertex arachno: n + 3 skeletal orbitals, 2n + 6 skeletal electrons

n-vertex hypho: n + 4 skeletal orbitals, 2n + 8 skeletal electrons

The skeletal electron counts are determined by summing the total of the following number of electrons:

2 from each BH unit

3 from each CH unit

1 from each additional hydrogen atom (over and above the ones on the BH and CH units)

the anionic charge electrons

5n rules

As discussed previously, the 4n rule mainly deals with clusters with electron counts of 4n + k, in which approximately 4 electrons are on each vertex. As more electrons are added per vertex, the number of the electrons per vertex approaches 5. Rather than adopting structures based on deltahedra, the 5n-type clusters have structures based on a different series of polyhedra known as the 3-connected polyhedra, in which each vertex is connected to 3 other vertices. The 3-connected polyhedra are the duals of the deltahedra. The common types of 3-connected polyhedra are listed below.

The 5n rules are as follows.

Example: P₄

Electron count: 4 × P = 4 × 5 = 20 It is a 5n structure with n = 4, so it is tetrahedral

Example: P₄S₃

Electron count 4 × P + 3 × S = 4 × 5 + 3 × 6 = 38 It is a 5n + 3 structure with n = 7. Three vertices are inserted into edges

Example: P₄O₆

Electron count 4 × P + 6 × O = 4 × 5 + 6 × 6 = 56 It is a 5n + 6 structure with n = 10. Six vertices are inserted into edges

6n rules

As more electrons are added to a 5n cluster, the number of electrons per vertex approaches 6. Instead of adopting structures based on 4n or 5n rules, the clusters tend to have structures governed by the 6n rules, which are based on rings. The rules for the 6n structures are as follows.

Example: S₈

Electron count = 8 × S = 8 × 6 = 48 electrons. Since n = 8, 6n = 48, so the cluster is an 8-membered ring.

Hexane (C₆H₁₄)

Electron count = 6 × C + 14 × H = 6 × 4 + 14 × 1 = 38 Since n = 6, 6n = 36 and 6n + 2 = 38, so the cluster is a 6-membered chain.

Isolobal vertex units

Provided a vertex unit is isolobal with BH then it can, in principle at least, be substituted for a BH unit, even though BH and CH are not isoelectronic. The CH⁺ unit is isolobal, hence the rules are applicable to carboranes. This can be explained due to a frontier orbital treatment. Additionally there are isolobal transition-metal units. For example, Fe(CO)₃ provides 2 electrons. The derivation of this is briefly as follows:

Fe has 8 valence electrons.

Each carbonyl group is a net 2 electron donor after the internal σ- and π-bonding are taken into account making 14 electrons.

3 pairs are considered to be involved in Fe–CO σ-bonding and 3 pairs are involved in π-backbonding from Fe to CO reducing the 14 to 2.

Polyhedron

B₂H₆

The bonding in diborane is best described by treating each B as sp³-hybridized. Two sp³-hybrid orbitals on each boron form the bonds to the terminal hydrogens. The remaining sp³-orbitals create the bonds with the bridging hydrogens. Because the angles in the diborane structure are not tetrahedral the orbitals also likely contain some sp² character.

closo-B
6H2−
6

The boron atoms lie on each vertex of the octahedron and are sp hybridized. One sp-hybrid radiates away from the structure forming the bond with the hydrogen atom. The other sp-hybrid radiates into the center of the structure forming a large bonding molecular orbital at the center of the cluster. The remaining two unhybridized orbitals lie along the tangent of the sphere like structure creating more bonding and antibonding orbitals between the boron vertices. The orbital diagram breaks down as follows: The total skeletal bonding orbitals is therefore 7, i.e. n + 1.

Main group atom clusters

The bonding in other main group cluster compounds follow similar rules as those described for the boron cluster bonding. The atoms at the vertex hybridize in a way which allows the lowest energy structure to form. The 18 framework molecular orbitals, (MOs), derived from the 18 boron atomic orbitals are:

1 bonding MO at the center of the cluster and 5 antibonding MOs from the 6 sp-radial hybrid orbitals

6 bonding MOs and 6 antibonding MOs from the 12 tangential p-orbitals.

The total skeletal bonding orbitals is therefore 7, i.e. n + 1.

Transition metal clusters

Transition metal clusters use the d orbitals for bonding so have up to nine bonding orbitals, instead of only the four present in boron and main group clusters. There is also more bonding flexibility in transition metal clusters depending on whether vertex metal electron pairs are involved in cluster bonding or appear as lone pairs. The cluster chlorides and carbonyls of transition metals will be briefly discussed here as they represent opposite ends of the spectrochemical series and show important features of the differences between transition metal clusters with different ligands. In chloride clusters the energy splitting of the valence d orbitals increases upon formation of the cluster. The number and symmetry of these orbitals are dependent upon the type and structure of each individual cluster complex. Conversely in the carbonyl clusters the energy splitting of the valence d orbitals is greater before the formation of the cluster.

MO diagram clusters metal chlorides and metal carbonyls