 | ||
In mathematics, in functional analysis, several different wavelets are known by the name Poisson wavelet. In one context, the term "Poisson wavelet" is used to denote a family of wavelets labeled by the set of positive integers, the members of which are associated with the Poisson probability distribution. These wavelets were first defined and studied by Karlene A. Kosanovich, Allan R. Moser and Michael J. Piovoso in 1995–96. In another context, the term refers to a certain wavelet which involves a form of the Poisson integral kernel. In a still another context, the terminology is used to describe a family of complex wavelets indexed by positive integers which are connected with the derivatives of the Poisson integral kernel.
Contents
Definition
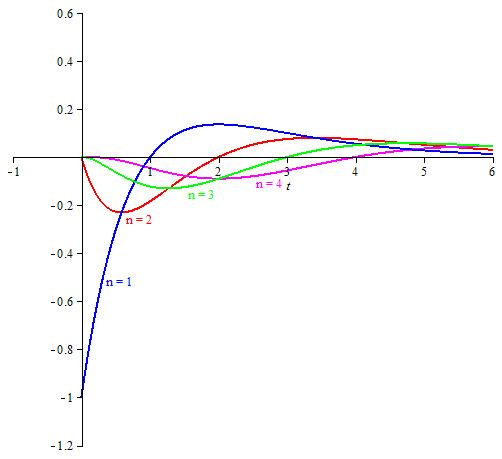
For each positive integer n the Poisson wavelet
To see the relation between the Poisson wavelet and the Poisson distribution let X be a discrete random variable having the Poisson distribution with parameter (mean) t and, for each non-negative integer n, let Prob(X = n) = pn(t). Then we have
The Poisson wavelet
Basic properties
Poisson wavelet transform
The Poisson wavelet family can be used to construct the family of Poisson wavelet transforms of functions defined the time domain. Since the Poisson wavelets satisfy the admissibility condition also, functions in the time domain can be reconstructed from their Poisson wavelet transforms using the formula for inverse continuous-time wavelet transforms.
If f(t) is a function in the time domain its n-th Poisson wavelet transform is given by
In the reverse direction, given the n-th Poisson wavelet transform
Applications
Poisson wavelet transforms have been applied in multi-resolution analysis, system identification, and parameter estimation. They are particularly useful in studying problems in which the functions in the time domain consist of linear combinations of decaying exponentials with time delay.
Definition
The Poisson wavelet is defined by the function
This can be expressed in the form
Relation with Poisson kernel
The function
This is the initial value problem: Given any
-
∫ − ∞ ∞ | ϕ ( x , y ) | p d x ≤ c < ∞ , and -
ϕ ( x , y ) → s ( x ) asy → 0 inL p ( R ) .
The problem has the following solution: There is exactly one function
where
Properties
Definition
The Poisson wavelet is a family of complex valued functions indexed by the set of positive integers and defined by
Relation with Poisson kernel
The function
Writing the function
we have
Thus
Properties
The Fourier transform of
where
