 | ||
In mathematics and especially in combinatorics, a plane partition is a two-dimensional array of nonnegative integers
Contents
- Ferrers diagrams for plane partitions
- Equivalence of the two representations
- Action of S3 on plane partitions
- Generating function
- MacMahon formula
- Asymptotics of plane partitions
- Symmetries
- References
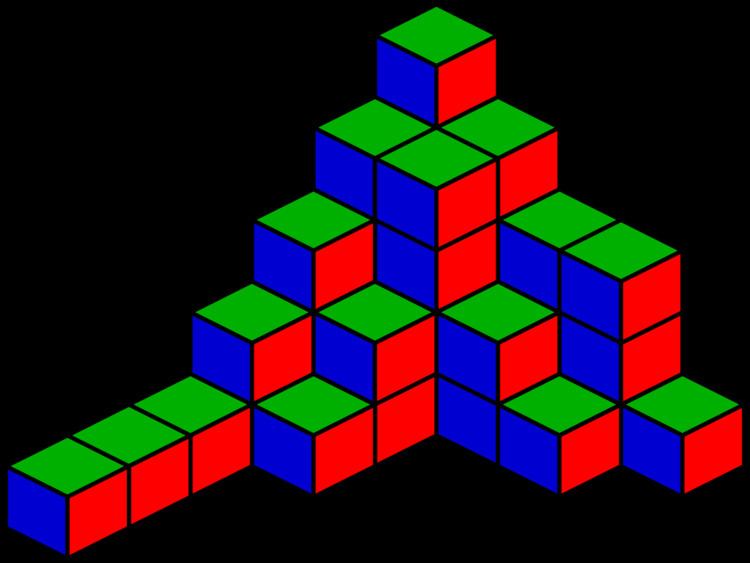
and for which only finitely many of the ni,j are nonzero. A plane partitions may be represented visually by the placement of a stack of
The sum of a plane partition is
and PL(n) denotes the number of plane partitions with sum n.
For example, there are six plane partitions with sum 3:
so PL(3) = 6. (Here the plane partitions are drawn using matrix indexing for the coordinates and the entries equal to 0 are suppressed for readability.)
Ferrers diagrams for plane partitions
Another representation for plane partitions is in the form of Ferrers diagrams. The Ferrers diagram of a plane partition of
Replacing every node of a plane partition by a unit cube with edges aligned with the axes leads to the stack of cubes representation for the plane partition.
Equivalence of the two representations
Given a Ferrers diagram, one constructs the plane partition (as in the main definition) as follows.
LetGiven a set of
For instance, below we show the two representations of a plane partitions of 5.
Above, every node of the Ferrers diagram is written as a column and we have only written only the non-vanishing
Action of S3 on plane partitions
There is a natural action of the permutation group
Generating function
By a result of Percy MacMahon, the generating function for PL(n) is given by
This is sometimes referred to as the MacMahon function.
This formula may be viewed as the 2-dimensional analogue of Euler's product formula for the number of integer partitions of n. There is no analogous formula known for partitions in higher dimensions (i.e., for solid partitions).
MacMahon formula
Denote by
MacMahon formula is the multiplicative formula for general values of
This formula was obtained by Percy MacMahon and was later rewritten in this form by Ian Macdonald.
Asymptotics of plane partitions
The asymptotics of plane partitions was worked out by E. M. Wright. One has, for large
where we have corrected for the typographical error (in Wright's paper) pointed out by Mutafchiev and Kamenov. Evaluating numerically, one finds
Symmetries
Plane partitions may be classified according to various symmetries. When viewed as a two-dimensional array of integers, there is the natural symmetry of conjugation or transpose that corresponds to switching the indices i and j; for example, the two plane partitions
are conjugate. When viewed as three-dimensional arrays of blocks, however, more symmetries become evident: any permutation of the axes corresponds to a reflection or rotation of the plane partition. A plane partition that is invariant under all of these symmetries is called totally symmetric.
An additional symmetry is complementation: given a plane partition inside an
