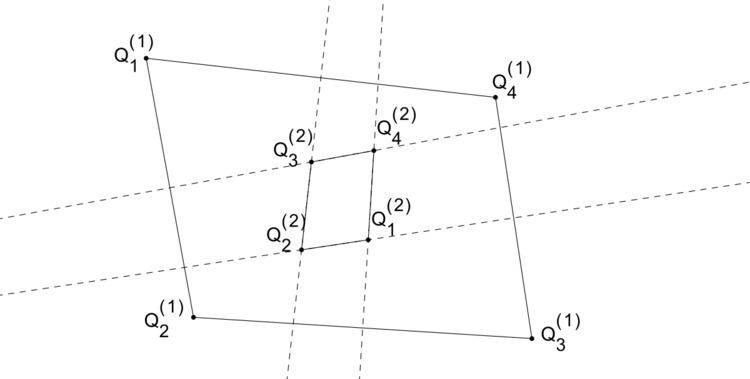
In geometry, the perpendicular bisector construction of a quadrilateral is a construction which produces a new quadrilateral from a given quadrilateral using the perpendicular bisectors to the sides of the former quadrilateral. This construction arises naturally in an attempt to find a replacement for the circumcenter of a quadrilateral in the case that is non-cyclic.
Suppose that the vertices of the quadrilateral Q are given by Q 1 , Q 2 , Q 3 , Q 4 . Let b 1 , b 2 , b 3 , b 4 be the perpendicular bisectors of sides Q 1 Q 2 , Q 2 Q 3 , Q 3 Q 4 , Q 4 Q 1 respectively. Then their intersections Q i ( 2 ) = b i + 2 b i + 3 , with subscripts considered modulo 4, form the consequent quadrilateral Q ( 2 ) . The construction is then iterated on Q ( 2 ) to produce Q ( 3 ) and so on.
An equivalent construction can be obtained by letting the vertices of Q ( i + 1 ) be the circumcenters of the 4 triangles formed by selecting combinations of 3 vertices of Q ( i ) .
1. If Q ( 1 ) is not cyclic, then Q ( 2 ) is not degenerate.
2. Quadrilateral Q ( 2 ) is never cyclic. Combining #1 and #2, Q ( 3 ) is always nondegenrate.
3. Quadrilaterals Q ( 1 ) and Q ( 3 ) are homothetic, and in particular, similar. Quadrilaterals Q ( 2 ) and Q ( 4 ) are also homothetic.
3. The perpendicular bisector construction can be reversed via isogonal conjugation. That is, given Q ( i + 1 ) , it is possible to construct Q ( i ) .
4. Let α , β , γ , δ be the angles of Q ( 1 ) . For every i , the ratio of areas of Q ( i ) and Q ( i + 1 ) is given by
( 1 / 4 ) ( cot ( α ) + cot ( γ ) ) ( cot ( β ) + cot ( δ ) ) . 5. If Q ( 1 ) is convex then the sequence of quadrilaterals Q ( 1 ) , Q ( 2 ) , … converges to the isoptic point of Q ( 1 ) , which is also the isoptic point for every Q ( i ) . Similarly, if Q ( 1 ) is concave, then the sequence Q ( 1 ) , Q ( 0 ) , Q ( − 1 ) , … obtained by reversing the construction converges to the Isoptic Point of the Q ( i ) 's.