Faces 10 triangles Vertices 7 | Edges 15 Schläfli symbol { } + {5} | |
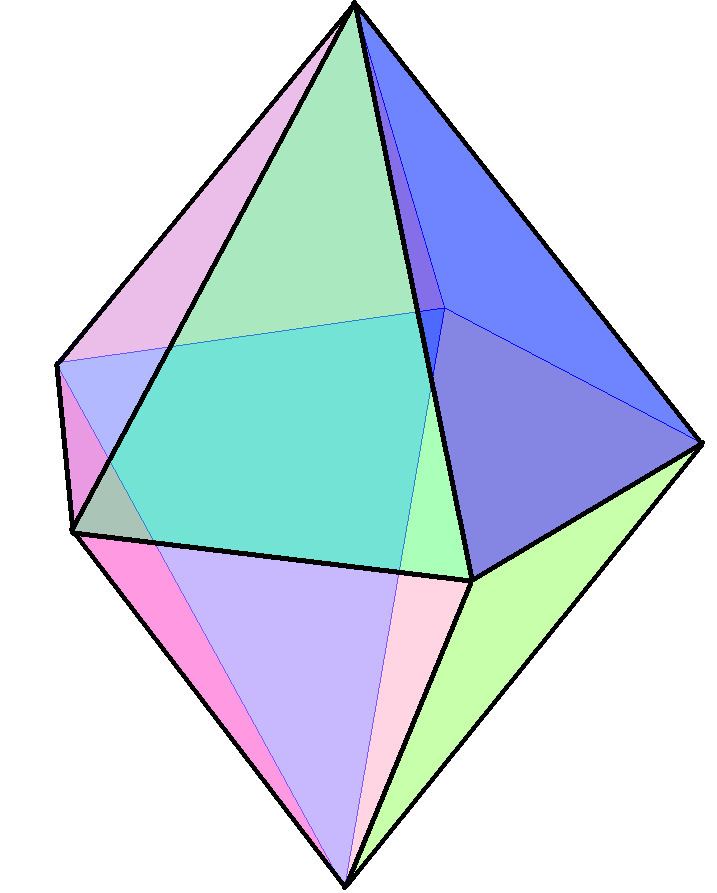 | ||
Type Bipyramid
and
Johnson
J12 - J13 - J14 Symmetry group D5h, [5,2], (*225), order 20 | ||
In geometry, the pentagonal bipyramid (or dipyramid) is third of the infinite set of face-transitive bipyramids. Each bipyramid is the dual of a uniform prism.
Contents
Although it is face-transitive, it is not a Platonic solid because some vertices have four faces meeting and others have five faces.
Properties
If the faces are equilateral triangles, it is a deltahedron and a Johnson solid (J13). It can be seen as two pentagonal pyramids (J2) connected by their bases.
A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
The pentagonal dipyramid is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the regular octahedron, the snub disphenoid, and an irregular polyhedron with 12 vertices and 20 triangular faces.
Related polyhedra
The pentagonal bipyramid, dt{2,5}, can be in sequence rectified, rdt{2,5}, truncated, trdt{2,5} and alternated (snubbed), srdt{2,5}:
The dual of the Johnson solid pentagonal bipyramid is the pentagonal prism, with 7 faces: 5 rectangular faces and 2 pentagons.
