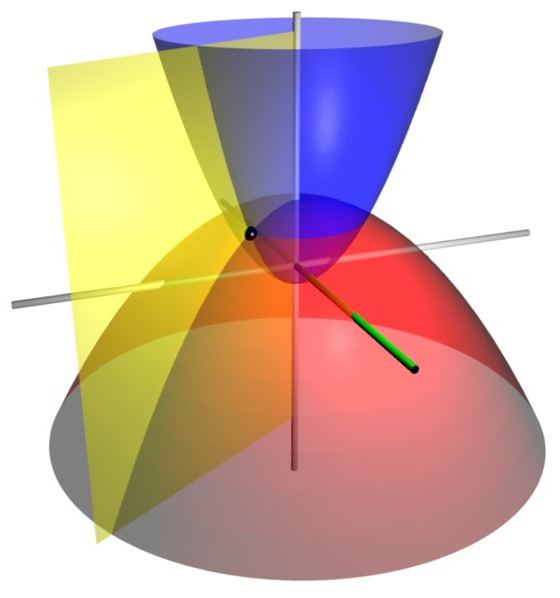
Paraboloidal coordinates are a three-dimensional orthogonal coordinate system ( λ , μ , ν ) that generalizes the two-dimensional parabolic coordinate system. Similar to the related ellipsoidal coordinates, the paraboloidal coordinate system has orthogonal quadratic coordinate surfaces that are not produced by rotating or projecting any two-dimensional orthogonal coordinate system.
The Cartesian coordinates ( x , y , z ) can be produced from the ellipsoidal coordinates ( λ , μ , ν ) by the equations
x 2 = ( A − λ ) ( A − μ ) ( A − ν ) B − A y 2 = ( B − λ ) ( B − μ ) ( B − ν ) A − B z = 1 2 ( A + B − λ − μ − ν ) where the following limits apply to the coordinates
λ < B < μ < A < ν Consequently, surfaces of constant λ are elliptic paraboloids
x 2 λ − A + y 2 λ − B = 2 z + λ and surfaces of constant ν are likewise
x 2 ν − A + y 2 ν − B = 2 z + ν whereas surfaces of constant μ are hyperbolic paraboloids
x 2 μ − A + y 2 μ − B = 2 z + μ The scale factors for the paraboloidal coordinates ( λ , μ , ν ) are
h λ = 1 2 ( μ − λ ) ( ν − λ ) ( A − λ ) ( B − λ ) h μ = 1 2 ( ν − μ ) ( λ − μ ) ( A − μ ) ( B − μ ) h ν = 1 2 ( λ − ν ) ( μ − ν ) ( A − ν ) ( B − ν ) Hence, the infinitesimal volume element equals
d V = ( μ − λ ) ( ν − λ ) ( ν − μ ) 8 ( A − λ ) ( B − λ ) ( A − μ ) ( μ − B ) ( ν − A ) ( ν − B ) d λ d μ d ν Differential operators such as ∇ ⋅ F and ∇ × F can be expressed in the coordinates ( λ , μ , ν ) by substituting the scale factors into the general formulae found in orthogonal coordinates.