Supriya Ghosh (Editor)

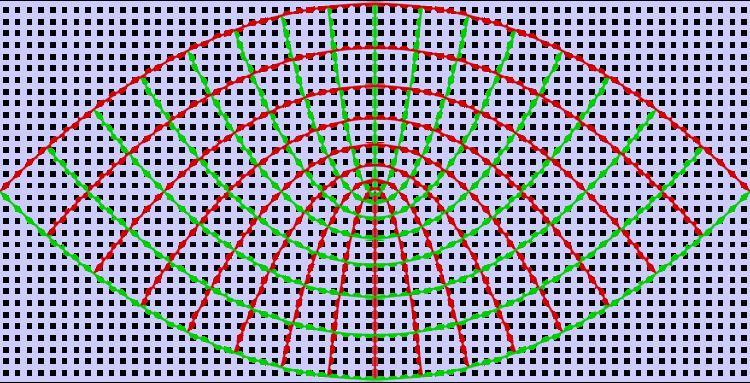
Parabolic coordinates

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Parabolic coordinates

Parabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.

Contents

Parabolic coordinates have found many applications, e.g., the treatment of the Stark effect and the potential theory of the edges.

Two-dimensional parabolic coordinates

Two-dimensional parabolic coordinates ( σ , τ ) are defined by the equations, in terms of cartesian coordinates:

x = σ τ y = 1 2 ( τ 2 − σ 2 )

The curves of constant σ form confocal parabolae

2 y = x 2 σ 2 − σ 2

that open upwards (i.e., towards + y ), whereas the curves of constant τ form confocal parabolae

2 y = − x 2 τ 2 + τ 2

that open downwards (i.e., towards − y ). The foci of all these parabolae are located at the origin.

Two-dimensional scale factors

The scale factors for the parabolic coordinates ( σ , τ ) are equal

h σ = h τ = σ 2 + τ 2

Hence, the infinitesimal element of area is

d A = ( σ 2 + τ 2 ) d σ d τ

and the Laplacian equals

∇ 2 Φ = 1 σ 2 + τ 2 ( ∂ 2 Φ ∂ σ 2 + ∂ 2 Φ ∂ τ 2 )

Other differential operators such as ∇ ⋅ F and ∇ × F can be expressed in the coordinates ( σ , τ ) by substituting the scale factors into the general formulae found in orthogonal coordinates.

Three-dimensional parabolic coordinates

The two-dimensional parabolic coordinates form the basis for two sets of three-dimensional orthogonal coordinates. The parabolic cylindrical coordinates are produced by projecting in the z -direction. Rotation about the symmetry axis of the parabolae produces a set of confocal paraboloids, the coordinate system of tridimensional parabolic coordinates. Expressed in terms of cartesian coordinates:

x = σ τ cos ⁡ φ y = σ τ sin ⁡ φ z = 1 2 ( τ 2 − σ 2 )

where the parabolae are now aligned with the z -axis, about which the rotation was carried out. Hence, the azimuthal angle ϕ is defined

tan ⁡ φ = y x

The surfaces of constant σ form confocal paraboloids

2 z = x 2 + y 2 σ 2 − σ 2

that open upwards (i.e., towards + z ) whereas the surfaces of constant τ form confocal paraboloids

2 z = − x 2 + y 2 τ 2 + τ 2

that open downwards (i.e., towards − z ). The foci of all these paraboloids are located at the origin.

The Riemannian metric tensor associated with this coordinate system is

g i j = [ σ 2 + τ 2 0 0 0 σ 2 + τ 2 0 0 0 σ 2 τ 2 ]

Three-dimensional scale factors

The three dimensional scale factors are:

h σ = σ 2 + τ 2 h τ = σ 2 + τ 2 h φ = σ τ

It is seen that The scale factors h σ and h τ are the same as in the two-dimensional case. The infinitesimal volume element is then

d V = h σ h τ h φ d σ d τ d φ = σ τ ( σ 2 + τ 2 ) d σ d τ d φ

and the Laplacian is given by

∇ 2 Φ = 1 σ 2 + τ 2 [ 1 σ ∂ ∂ σ ( σ ∂ Φ ∂ σ ) + 1 τ ∂ ∂ τ ( τ ∂ Φ ∂ τ ) ] + 1 σ 2 τ 2 ∂ 2 Φ ∂ φ 2

Other differential operators such as ∇ ⋅ F and ∇ × F can be expressed in the coordinates ( σ , τ , ϕ ) by substituting the scale factors into the general formulae found in orthogonal coordinates.

References

Parabolic coordinates Wikipedia
(Text) CC BY-SA