POVM - Alchetron, The Free Social Encyclopedia

In functional analysis and quantum measurement theory, a positive-operator valued measure (POVM) is a measure whose values are non-negative self-adjoint operators on a Hilbert space, and whose integral is the identity operator. It is the most general formulation of a measurement in the theory of quantum physics. The need for the POVM formalism arises from the fact that projective measurements on a larger system, by which we mean measurements that are performed mathematically by a projection-valued measure (PVM), will act on a subsystem in ways that cannot be described by a PVM on the subsystem alone. POVMs are used in the field of quantum information.

In rough analogy, a POVM is to a PVM what a density matrix is to a pure state. Density matrices are needed to specify the state of a subsystem of a larger system, even when the larger system is in a pure state (see purification of quantum state); analogously, POVMs on a physical system are used to describe the effect of a projective measurement performed on a larger system.

Historically, the term probability-operator measure (POM) has been used as a synonym for POVM, although this usage is now rare.

Definition

In the simplest case, a POVM is a set of Hermitian positive semidefinite operators { F i } on a Hilbert space H that sum to the identity operator,

∑ i = 1 n F i = I H .

This formula is a generalization of the decomposition of a (finite-dimensional) Hilbert space by a set of orthogonal projectors, { E i } , defined for an orthogonal basis { | ϕ i ⟩ } by:

∑ i = 1 N E i = I H , E i E j = δ i j E i , E i = | ϕ i ⟩ ⟨ ϕ i | .

An important difference is that the elements of a POVM are not necessarily orthogonal, with the consequence that the number of elements in the POVM, n, can be larger than the dimension, N, of the Hilbert space they act in.

In general, POVMs can be defined in situations where the outcomes of measurements take values in a non-discrete space. The relevant fact is that measurement determines a probability measure on the outcome space:

Definition. Let (X, M) be measurable space; that is M is a σ-algebra of subsets of X. A POVM is a function F defined on M whose values are bounded non-negative self-adjoint operators on a Hilbert space H such that F(X) = I_H and for every ξ ∈ H,

E ↦ ⟨ F ( E ) ξ ∣ ξ ⟩

is a non-negative countably additive measure on the σ-algebra M.

This definition should be contrasted with that of the projection-valued measure, which is similar, except that for projection-valued measures, the values of F are required to be projection operators.

Neumark's dilation theorem

Note: An alternate spelling of this is "Naimark's Theorem"

Neumark's dilation theorem is a result that expresses POVMs in terms of projection-valued measures. It states that a POVM can be "lifted" by an operator map of the form V* (·)V to a projection-valued measure. In the physical context, this means that the measurements accomplished by a POVM consisting of a weighted sum of n rank-one operators acting on an N-dimensional Hilbert space (where one may typically have n > N) can equally well be achieved by performing a projective measurement on a Hilbert space of dimension n.

So, for example, as in the theory of projective measurement, the probability that the outcome associated with measurement of operator F i occurs

P ( i ) = t r ( ρ F i ) ,

where ρ is the density matrix representing the mixed state of the measured system.

Such a measurement can be carried out by doing a projective measurement in a larger Hilbert space. Let us extend the Hilbert space H A to H A ⊕ H A ⊥ and perform the measurement defined by the projection operators { π ^ i } . The probability of the outcome associated with π ^ i is

P ( i ) = t r ( ρ π ^ i ) = t r ( ρ π ^ A π ^ i π ^ A ) ,

where π ^ A is the orthogonal projection taking H A ⊕ H A ⊥ to H A . In the original Hilbert space H A , this is a POVM with operators given by F i = π ^ A π ^ i π ^ A . Neumark's dilation theorem guarantees that any POVM can be implemented in this manner.

In practice, POVMs are usually performed by coupling the original system to an ancilla. For an ancilla prepared in a pure state | 0 ⟩ B , this is a special case of the above; the Hilbert space is extended by the states | ϕ ⟩ A ⊗ | ψ ⟩ B where ⟨ ψ | 0 ⟩ B = 0 .

Post-measurement state

Consider the case where the ancilla is initially a pure state | 0 ⟩ B . We entangle the ancilla with the system, taking

| ψ ⟩ A | 0 ⟩ B → ∑ i M i | ψ ⟩ A | i ⟩ B ,

and perform a projective measurement on the ancilla in the { | i ⟩ B } basis. The operators of the resulting POVM are given by

F i = M i † M i .

Since the M i are not required to be positive, there are an infinite number of solutions to this equation. This means that there are infinite different experimental apparatuses that give the same probabilities for the outcomes. Since the post-measurement state of the system

ρ ′ = M i ρ M i † t r ( M i ρ M i † )

depends on the M i , in general it cannot be inferred from the POVM alone.

Another difference from the projective measurements is that a POVM is not repeatable. If ρ ′ is subjected to the same measurement, the new state is

ρ ″ = M i ρ ′ M i † t r ( M i ρ ′ M i † ) = M i M i ρ M i † M i † t r ( M i M i ρ M i † M i † )

which is equal to ρ ′ iff M i 2 = M i , that is, if the POVM reduces to a projective measurement.

This gives rises to many interesting effects, amongst them the quantum anti-Zeno effect.

Quantum properties of measurements

A recent work by T. Amri makes the claim that the properties of a measurement are not revealed by the POVM element corresponding to the measurement, but by its pre-measurement state. This one is the main tool of the retrodictive approach of quantum physics in which we make predictions about state preparations leading to a measurement result. We show, that this state simply corresponds to the normalized POVM element:

ρ ^ r e t r [ n ] = Π ^ n T r { Π ^ n } .

We can make predictions about preparations leading to the result 'n' by using an expression similar to Born's rule:

P r ( m | n ) = T r { ρ ^ r e t r [ n ] Θ ^ m } ,

in which Θ ^ m is a hermitian and positive operator corresponding to a proposition about the state of the measured system just after its preparation in some a state ρ ^ m . Such an approach allows us to determine in which kind of states the system was prepared for leading to the result 'n'.

Thus, the non-classicality of a measurement corresponds to the non-classicality of its pre-measurement state, for which such a notion can be measured by different signatures of non-classicality. The projective character of a measurement can be measured by its projectivity π n which is the purity of its pre-measurement state:

π n = T r [ ( ρ ^ r e t r [ n ] ) 2 ] .

The measurement is projective when its pre-measurement state is a pure quantum state | ψ n ⟩ ( π n = 1 ) . Thus, the corresponding POVM element is given by:

Π ^ n = η n | ψ n ⟩ ⟨ ψ n | ,

where η n = T r { Π n } is in fact the detection efficiency of the state | ψ n ⟩ , since Born's rule leads to P r ( n | ψ n ) = η n . Therefore, the measurement can be projective but non-ideal, which is an important distinction with the usual definition of projective measurements.

An example: Unambiguous quantum state discrimination

Let us suppose that a quantum system (which we call the input) is known to be in a state drawn randomly from a given set of pure states. The task of unambiguous quantum state discrimination (UQSD) is to discern conclusively, at least sometimes, which state the system was in. The impossibility of perfectly discriminating between a set of non-orthogonal states is the basis for quantum information protocols such as quantum cryptography, quantum coin-flipping, and quantum money.

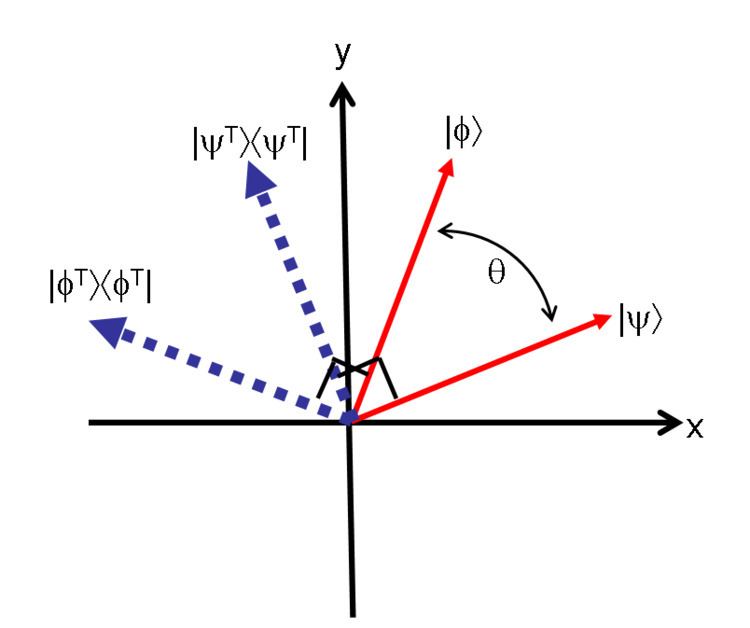
We will give a 2-dimensional example in which using a POVM strategy has a higher success probability for achieving UQSD than any possible projective measurement.

First, consider a trivial case. Take a set consisting of two orthogonal states | ψ ⟩ and | ψ T ⟩ . A projective measurement whose corresponding Hermitian operator has the form

A ^ = a | ψ T ⟩ ⟨ ψ T | + b | ψ ⟩ ⟨ ψ | ,

will result in eigenvalue a only when the system is in | ψ T ⟩ and eigenvalue b only when the system is in | ψ ⟩ . In addition, the measurement always discriminates between the two states (i.e. with 100% probability). So we can achieve UQSD every single time. This is impossible for anything but orthogonal states.

Now consider a set that consists of two states | ψ ⟩ and | ϕ ⟩ in two-dimensional Hilbert space that are not orthogonal. i.e.,

| ⟨ ϕ | ψ ⟩ | = cos ⁡ ( θ ) ,

for θ > 0 . These could be states of a system such as the spin of spin-1/2 particle (e.g. an electron), or the polarization of a photon.

In order to make a quantitative comparison between different strategies, we make the a-priori assumption that the system has an equal likelihood of being in each of these two permitted states. Then the best strategy for UQSD using only projective measurement is to perform each of the following measurements,

π ^ ψ T = | ψ T ⟩ ⟨ ψ T | , π ^ ϕ T = | ϕ T ⟩ ⟨ ϕ T | ,

50% of the time. Here the "T" indicates a vector orthogonal to the given vector. Being projections, these observables have possible outcomes of 0 or 1. If the measurement π ^ ψ T is performed and results in a value of 1, then it is certain that the state was in | ϕ ⟩ . However, a result of 0 is inconclusive since this can come from the system being in either of the two states in the set. Similarly, a result of 1 for the measurement π ^ ϕ T indicates conclusively that the system was in | ψ ⟩ and a result of 0 is inconclusive. The probability that this strategy returns a conclusive result is then,

P p r o j = 1 − | ⟨ ϕ | ψ ⟩ | 2 2 .

As we shall see, a strategy based on POVMs has a greater probability of success given by,

P P O V M = 1 − | ⟨ ϕ | ψ ⟩ | .

This is the minimum allowed by the rules of quantum indeterminacy and the uncertainty principle. This strategy is based on a POVM consisting of,

F ^ ψ = 1 − | ϕ ⟩ ⟨ ϕ | 1 + | ⟨ ϕ | ψ ⟩ | F ^ ϕ = 1 − | ψ ⟩ ⟨ ψ | 1 + | ⟨ ϕ | ψ ⟩ | F ^ i n c o n c l . = 1 − F ^ ψ − F ^ ϕ ,

where the result associated with F ^ i indicates the system is in state i with certainty.

These POVMs can be created by extending the two-dimensional Hilbert space. This can be visualized as follows: The two states fall in the x-y plane with an angle of θ between them and the space is extended in the z-direction. (The total space is the direct sum of spaces defined by the z-direction and the x-y plane.) The measurement first unitarily rotates the states towards the z-axis so that | ψ ⟩ has no component along the y-direction and | ϕ ⟩ has no component along the x-direction. At this point, the three elements of the POVM correspond to projective measurements along x-direction, y-direction and z-direction, respectively.

For a specific example, take a stream of photons, each of which is polarized along either the horizontal direction or at 45 degrees. On average there are equal numbers of horizontal and 45 degree photons. The projective strategy corresponds to passing the photons through a polarizer in either the vertical direction or -45 degree direction. If the photon passes through the vertical polarizer it must have been at 45 degrees and vice versa. The success probability is ( 1 − 1 / 2 ) / 2 = 25 % . The POVM strategy for this example is more complicated and requires another optical mode (known as an ancilla). It has a success probability of 1 − 1 / 2 = 29.3 % .

SIC-POVM

Quantum t-designs have been recently introduced to POVMs and symmetric, informationally-complete POVM's (SIC-POVM's) as a means of providing a simple and elegant formulation of the field in a general setting, since a SIC-POVM is a type of spherical t-design.

References

POVM Wikipedia

(Text) CC BY-SA

Contents