Oscillation (mathematics) - Alchetron, the free social encyclopedia

In mathematics, the oscillation of a function or a sequence is a number that quantifies how much a sequence or function varies between its extreme values as it approaches infinity or a point. As is the case with limits there are several definitions that put the intuitive concept into a form suitable for a mathematical treatment: oscillation of a sequence of real numbers, oscillation of a real valued function at a point, and oscillation of a function on an interval (or open set).

Oscillation of a sequence

Let ( a n ) be a sequence of real numbers. The oscillation ω ( a n ) of that sequence is defined as the difference (possibly infinite) between the limit superior and limit inferior of ( a n ) :

ω ( a n ) = lim sup n → ∞ a n − lim inf n → ∞ a n .

The oscillation is zero if and only if the sequence converges. It is undefined if lim sup n → ∞ and lim inf n → ∞ are both equal to +∞ or both equal to −∞, that is, if the sequence tends to +∞ or −∞.

Oscillation of a function on an open set

Let f be a real-valued function of a real variable. The oscillation of f on an interval I in its domain is the difference between the supremum and infimum of f :

ω f ( I ) = sup x ∈ I f ( x ) − inf x ∈ I f ( x ) .

More generally, if f : X → R is a function on a topological space X (such as a metric space), then the oscillation of f on an open set U is

ω f ( U ) = sup x ∈ U f ( x ) − inf x ∈ U f ( x ) .

Oscillation of a function at a point

The oscillation of a function f of a real variable at a point x 0 is defined as the limit as ϵ → 0 of the oscillation of f on an ϵ -neighborhood of x 0 :

ω f ( x 0 ) = lim ϵ → 0 ω f ( x 0 − ϵ , x 0 + ϵ ) .

This is the same as the difference between the limit superior and limit inferior of the function at x 0 , provided the point x 0 is not excluded from the limits.

More generally, if f : X → R is a real-valued function on a metric space, then the oscillation is

ω f ( x 0 ) = lim ϵ → 0 ω f ( B ϵ ( x 0 ) ) .

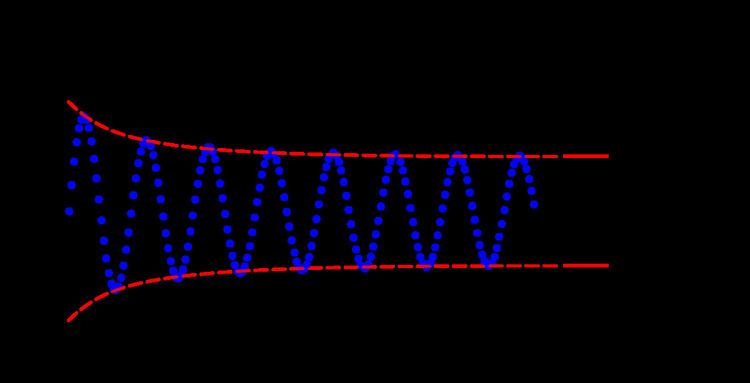
Examples

1/x has oscillation ∞ at x = 0, and oscillation 0 at other finite x and at −∞ and +∞.

sin (1/x) (the topologist's sine curve) has oscillation 2 at x = 0, and 0 elsewhere.

sin x has oscillation 0 at every finite x, and 2 at −∞ and +∞.

The sequence 1, −1, 1, −1, 1, −1, ... has oscillation 2.

In the last example the sequence is periodic, and any sequence that is periodic without being constant will have non-zero oscillation. However, non-zero oscillation does not usually indicate periodicity.

Geometrically, the graph of an oscillating function on the real numbers follows some path in the xy-plane, without settling into ever-smaller regions. In well-behaved cases the path might look like a loop coming back on itself, that is, periodic behaviour; in the worst cases quite irregular movement covering a whole region.

Continuity

Oscillation can be used to define continuity of a function, and is easily equivalent to the usual ε-δ definition (in the case of functions defined everywhere on the real line): a function ƒ is continuous at a point x₀ if and only if the oscillation is zero; in symbols, ω f ( x 0 ) = 0. A benefit of this definition is that it quantifies discontinuity: the oscillation gives how much the function is discontinuous at a point.

For example, in the classification of discontinuities:

in a removable discontinuity, the distance that the value of the function is off by is the oscillation;

in a jump discontinuity, the size of the jump is the oscillation (assuming that the value at the point lies between these limits from the two sides);

in an essential discontinuity, oscillation measures the failure of a limit to exist.

This definition is useful in descriptive set theory to study the set of discontinuities and continuous points – the continuous points are the intersection of the sets where the oscillation is less than ε (hence a G_δ set) – and gives a very quick proof of one direction of the Lebesgue integrability condition.

The oscillation is equivalence to the ε-δ definition by a simple re-arrangement, and by using a limit (lim sup, lim inf) to define oscillation: if (at a given point) for a given ε₀ there is no δ that satisfies the ε-δ definition, then the oscillation is at least ε₀, and conversely if for every ε there is a desired δ, the oscillation is 0. The oscillation definition can be naturally generalized to maps from a topological space to a metric space.

Generalizations

More generally, if f : X → Y is a function from a topological space X into a metric space Y, then the oscillation of f is defined at each x ∈ X by

ω ( x ) = inf { d i a m ( f ( U ) ) ∣ U i s a n e i g h b o r h o o d o f x }

References

Oscillation (mathematics) Wikipedia

(Text) CC BY-SA

Contents