 | ||
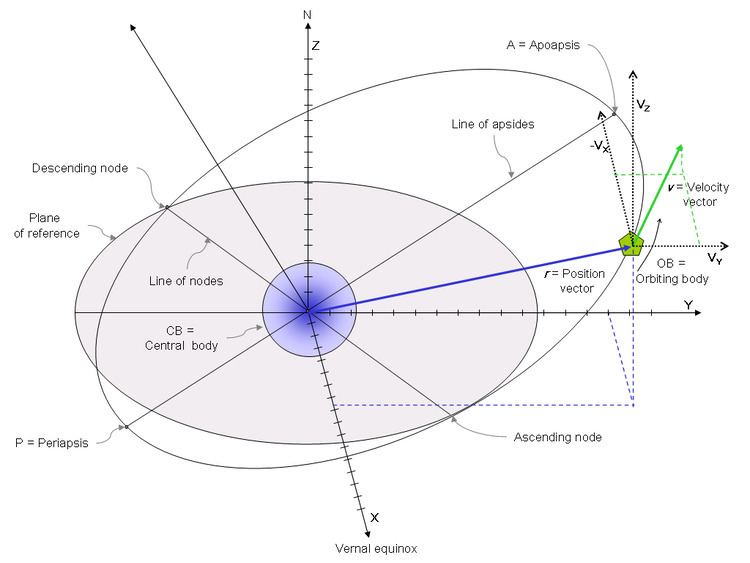
In astrodynamics and celestial dynamics, the orbital state vectors (sometimes state vectors) of an orbit are cartesian vectors of position (
Contents
Position vector
The position vector
The body does not actually have to be in orbit for its state vector to determine its trajectory; it only has to move ballistically, i.e., solely under the effects of its own inertia and gravity. For example, it could be a spacecraft or missile in a suborbital trajectory. If other forces such as drag or thrust are significant, they must be added vectorially to those of gravity when performing the integration to determine future position and velocity.
For any object moving through space, the velocity vector is tangent to the trajectory. If
Derivation
The velocity vector
An object's state vector can be used to compute its classical or Keplerian orbital elements and vice versa. Each representation has its advantages. The elements are more descriptive of the size, shape and orientation of an orbit, and may be used to quickly and easily estimate the object's state at any arbitrary time provided its motion is accurately modeled by the two-body problem with only small perturbations.
On the other hand, the state vector is more directly useful in a numerical integration that accounts for significant, arbitrary, time-varying forces such as drag, thrust and gravitational perturbations from third bodies as well as the gravity of the primary body.
The state vectors (
Because even satellites in low Earth orbit experience significant perturbations (primarily from Earth's non-spherical shape), the Keplerian elements computed from the state vector at any moment are only valid at that time. Such element sets are known as osculating elements because they coincide with the actual orbit only at that moment.
