Olog

Etymology

The term "olog" is short for "ontology log". "Ontology" derives from onto-, from the Greek ὤν, ὄντος "being; that which is", present participle of the verb εἰμί "be", and -λογία, -logia: science, study, theory.

Mathematical formalism

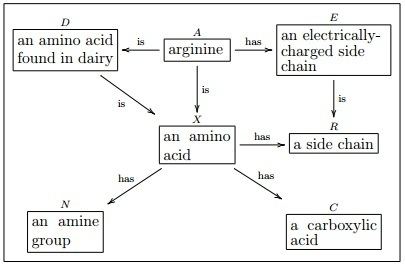
At the basic level an olog C is a category whose objects are represented as boxes containing sentences and whose morphisms are represented as directed labeled arrows between boxes. The structures of the sentences for both the objects and the morphisms of C need to be compatible with the mathematical definition of C . This compatibility cannot be checked mathematically, because it lies in the correspondence between mathematical ideas and natural language.

Every olog has a target category, which is taken to be Set (Category of sets), the category of sets and functions, unless otherwise mentioned. In that case, we are looking at a set of amino acids, a set of amine groups, and a function that assigns to every amino acid its amine group. In this article we usually stick to Set , though sometimes using the Kleisli category C P of the power set monad. Another possibility, though one we do not use here, would be to use the Kleisli category of probability distributions (the Giry monad), e.g., to obtain a generalization of Markov decision processes.

The boxes in the above example refer to objects of Set . For example, the box containing the sentence "an amino acid" refers to the set of all amino acids and the box containing the sentence "a side chain" refers to the set of all side chains. The arrow labeled with "has" whose source is "an amino acid" and whose target is "a side chain" refers to a morphism between two objects of Set and thus needs to be a function between two sets. Indeed, every amino acid has a unique side chain so the arrow is a valid morphism of Set . The functional nature of the morphisms in Set is expressed in an olog by labeling arrows with appropriate sentences (e.g. "has").

For another example let ( P , η , μ ) be the power set monad on Set so given A ∈ O b ( Set ) , P ( A ) is the power set of A, the natural transformation η sends a ∈ A to the singleton { a } and the natural transformation μ unionizes sets. A morphism f : A → B in the Kleisli category C P can be seen as establishing a binary relation R. Given a ∈ A and b ∈ B we say that ( a , b ) ∈ R if b ∈ f ( a ) .

We can use C P as the target category for an olog. In this case the arrows in the olog need to reflect the relational nature of morphisms in C P . This can be done by labeling every arrow in the olog with either "is related to", or "is greater than" and so on.

Ologs and databases

An olog C can also be viewed as a database schema. Every box (object of C ) in the olog is a table T and the arrows (morphisms) emanating from the box are columns in C . The assignment of a particular instance to an object of C is done through a functor I : C → Set . In the example above, the box "an amino acid" will be represented as a table whose number of rows is equal to the number of types of amino acids and whose number of columns is three, one column for each arrow emanating from that box.

Relations between ologs

Communication between different ologs which in practice can be communication between different models or world-views is done using functors. Spivak coins the notions of a 'meaningful' and 'strongly meaningful' functors. Let C and D be two ologs, I : C → Set , J : D → Set functors (see the section on ologs and databases) and F : C → D a functor. We say that a F is meaningful if there exists a natural transformation m : I → F ∗ J (the pullback of J by F).

Taking as an example C and D as two different scientific models, the functor F is meaningful if predictions, which are objects in Set , made by the first model C can be translated to the second model D .

We say that F is strongly meaningful if given an object X ∈ C we have I ( X ) = J ( F ( X ) ) . This equality is equivalent to requiring m to be a natural isomorphism.

Sometime it will be hard to find a meaningful functor F from C to D . In such a case we may try to define a new olog B which represents the common ground of C and D and find meaningful functors F C : B → C and F D : B → D .

If communication between ologs is limited to a two-way communication as described above then we may think of a collection of ologs as nodes of a graph and of the edges as functors connecting the ologs. If a simultaneous communication between more than two ologs is allowed then the graph becomes a symmetric simplicial complex.

Rules of good practice

Spivak provides some rules of good practice for writing an olog whose morphisms have a functional nature (see the first example in the section Mathematical formalism). The text in a box should adhere to the following rules:

1. begin with the word "a" or "an". (Example: "an amino acid").
2. refer to a distinction made and recognizable by the olog's author.
3. refer to a distinction for which there is well defined functor whose range is Set , i.e an instance can be documented. (Example: there is a set of all amino acids).
4. declare all variables in a compound structure. (Example: instead of writing in a box "a man and a woman" write "a man m and a woman w " or "a pair ( m , w ) where m is a man and w is a woman").

The first three rules ensure that the objects (the boxes) defined by the olog's author are well-defined sets. The fourth rule improves the labeling of arrows in an olog.

Applications

The concept was experimentally documented by David Spivak and coauthors Associate Professor Markus J. Buehler of the Department of Civil and Environmental Engineering (CEE) and CEE graduate student Tristan Giesa in a paper that was published in the December 2011 issue of BioNanoScience[2] in which the researchers establish a scientific analogy between spider silk and musical composition.