Nodal admittance matrix

Context

Electric power transmission needs optimization in order to determine the necessary real and reactive power flows in a system for a given set of loads, as well as the voltages and currents in the system. Power flow studies are used not only to analyze current power flow situations, but also to plan ahead for anticipated disturbances to the system, such as the loss of a transmission line to maintenance and repairs. The power flow study would determine whether or not the system could continue functioning properly without the transmission line. Only computer simulation allows the complex handling required in power flow analysis because in most realistic situations the system is very complex and extensive and would be impractical to solve by hand. The Y Matrix is a tool in that domain. It provides a method of systematically reducing a complex system to a matrix than can be solved by a computer program. The equations used to construct the Y matrix come from the application of Kirchhoff’s current law and Kirchhoff’s voltage law to a circuit with steady-state sinusoidal operation. These laws give us that the sum of currents entering a node in the circuit is zero, and the sum of voltages around a closed loop starting and ending at a node is also zero. These principles are applied to all the nodes in a power flow system and thereby determine the elements of the admittance matrix, which represents the admittance relationships between nodes, which then determine the voltages, currents and power flows in the system.

Construction

Starting from the single line diagram of a power system, there are three main steps before writing the equations that form the Y Matrix. First, the single line diagram is converted to an impedance diagram. Next, all voltage sources are converted to their equivalent current source representations. From here, the impedance diagram is then converted to an admittance diagram. Following these three steps, the admittance matrix can be created in a straightforward manner: For an admittance diagram with N buses, the admittance between the bus in consideration, k, and another bus, i, connected to k, can be described by y i k = g i k + j b i k . The term y k should be introduced here; this term accounts for the admittance of linear loads connected to bus k as well as the admittance-to-ground at bus k . The general mathematical expression follows:

It is important to note that y k i is non-zero only where a physical connection exists between two buses. This consideration is not seen in the following example because each node is connected to both of the other nodes. Each y k i defines one element of the N × N matrix. From the general case where N is greater than 2, it is desirable to solve these equations as a system, namely through matrix algebra. The general matrix appears as follows: The nodal admittance matrix form: Y = [ Y 11 Y 12 ⋯ Y 1 n Y 21 Y 22 ⋯ Y 2 n ⋯ ⋯ ⋯ ⋯ Y n 1 Y n 2 ⋯ Y n n ]

Once the admittance matrix has been formed, the admittance matrix can be input to solve the matrix form of Ohm's Law--the equation Y ∗ V = I . In this instance V is an N × 1 vector of the voltage at each node and I is the N x 1 vector of corresponding currents. In matrix form, Ohm's Law is as follows:

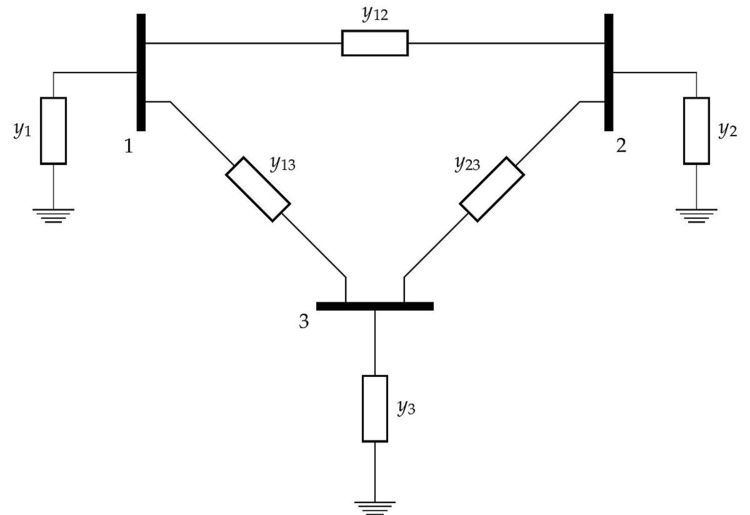
To illustrate this process with the admittance matrix of the three bus network in the figure would be:

The Y Matrix diagonal elements Y 11 , Y 22 , . . . , Y n n are called the self-admittances at the nodes, and each equals the sum of all the admittances terminating on the node identified by the repeated subscripts. The other admittances are the mutual admittances of the nodes, and each equals the negative of the sum of all admittances connected directly between the nodes identified by the double subscripts. The admittance matrix Y is typically a symmetric matrix as y m n = y n m . However, extensions of the line model and models of other components such as transformers may make Y asymmetrical.

For small transmission systems of about less than 10 nodes or buses, the Y matrix can be calculated manually. But for a realistic system with relatively large number of nodes or buses, say 1000 nodes, a computer program for computing Y is more practical to use.

To help motivate the importance of using a system of equations in matrix form, see the adjacent figure. Not only does it become impractical to calculate the current vector V by hand, it becomes necessary to use computational power to form the admittance matrix itself.

Example:

To take a look at a generalizable 2 × 2 matrix, consider the figure of the two-node network. By Kirchhoff's Current Law, it can be shown that : ( I m I n ) = ( 1 1 ) ∗ I a since there are no other currents entering or exiting nodes m or n . The voltage drop across the line can be expressed as : V a = ( 1 ∗ − 1 ) ∗ ( V m V n ) . Next, use Ohm's Law with admittance instead of impedance. Using substitution to get : ( Y a − Y a − Y a Y a ) ∗ ( V m V n ) = ( I m I n ) . To reintroduce some generality, Y 11 = Y m m , Y 21 = Y n m , Y 12 = Y m n , and Y 22 = Y n n . Thus, this example can be taken as a first step in understanding how to generally construct an N x N matrix by hand.