Supriya Ghosh (Editor)

Netoid function

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Netoid function

A netoid function which is a mathematical function having an "S" shape is generalized by the sigmoid function. It was defined by Robert Metcalfe in 2013. Then it was used by Zhang, Liu and Xu [1] to represent growth trend of the network size n with respect to time t. The netoid function is defined by the formula:

Contents

N e t o i d = p / ( 1 + e − v ∗ ( t − h ) )

The three parameters p,v, h have the following meanings:

  • p: the peak value representing the maximum value of the number of monthly active users (MAUs);
  • v: the virality or speed with which adoption occurs;
  • h: the point in time at which the growth rate is maximum, when the network size reaches half the peak.

    • Properties

    A Sigmoid function is defined by the formula: 1 / ( 1 + e − x ) . The range of x-axis is from negative infinity to positive infinity, y-axis represents the cumulative percentage at the value of x. When x tends to negative infinity, y tends to 0% and when x approaches to positive infinity, y approaches the maximum value of 100%. The sigmoid adoption rate peaks at x=0 with y of 50 percent.

    The Netoid function has the same S-curve shape as the sigmoid. Its slope (the adoption rate) is proportional to the product of the fraction of the population already adopted times the fraction awaiting adoption. It peaks when adoption is 50 percent. The adoption rate is driven by the number of adoptions so far and limited by the number of those awaiting adoption.

    Examples

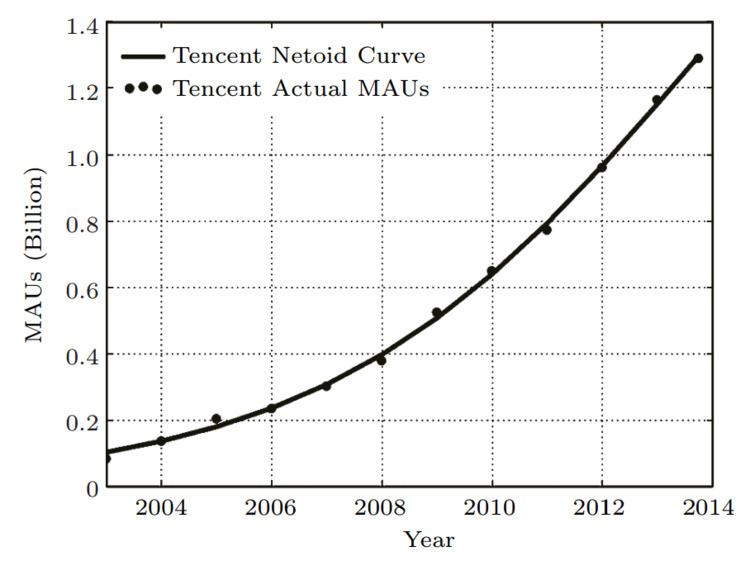
    Metcalfe used Facebook's data from 2003 to 2013 to show a good fit for the netoid function. Then Zhang, Liu and Xu use the actual data of Tencent (China's largest social network company) and Facebook to fit the netoid function. Their work show that the growth trend of MAUs of Tencent and Facebook over the past decade can be modeled by the netoid functions.

    The netoid functions are N e t o i d T e n c e n t = 2.61 ∗ 10 9 / ( 1 + e − 0.30 ∗ ( t − 2013.8 ) ) and N e t o i d F a c e b o o k = 1.45 ∗ 10 9 / ( 1 + e − 0.77 ∗ ( t − 2010.56 ) ) , respectively.

    References

    Netoid function Wikipedia
    (Text) CC BY-SA