Net force

Total force

The sum of forces acting on a particle is called the total force or the net force. The net force is a single force that replaces the effect of the original forces on the particle's motion. It gives the particle the same acceleration as all those actual forces together as described by the Newton's second law of motion.

Force is a vector quantity, which means that it has a magnitude and a direction, and it is usually denoted using boldface such as F or by using an arrow over the symbol, such as F → .

Graphically, a force is represented as line segment from its point of application A to a point B which defines its direction and magnitude. The length of the segment AB represents the magnitude of the force.

Vector calculus was developed in the late 1800s and early 1900s. The parallelogram rule used for the addition of forces, however, dates from antiquity and is noted explicitly by Galileo and Newton.

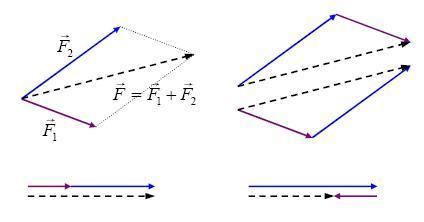
The diagram shows the addition of the forces F → 1 and F → 2 . The sum F → of the two forces is drawn as the diagonal of a parallelogram defined by the two forces.

Forces applied to an extended body can have different points of application. Forces are bound vectors and can be added only if they are applied at the same point. The net force obtained from all the forces acting on a body will not preserve its motion unless they are applied at the same point and the appropriate torque associated with the new point of application is determined. The net force on a body applied at a single point with the appropriate torque is known as the resultant force and torque.

Parallelogram rule for the addition of forces

A force is known as a bound vector which means it has a direction and magnitude and a point of application. A convenient way to define a force is by a line segment from a point A to a point B. If we denote the coordinates of these points as A=(A_x, A_y, A_z) and B=(B_x, B_y, B_z), then the force vector applied at A is given by

F = B − A = ( B x − A x , B y − A y , B z − A z ) .

The length of the vector B-A defines the magnitude of F and is given by

| F | = ( B x − A x ) 2 + ( B y − A y ) 2 + ( B z − A z ) 2 .

The sum of two forces F₁ and F₂ applied at A can be computed from the sum of the segments that define them. Let F₁=B-A and F₂=D-A, then the sum of these two vectors is

F = F 1 + F 2 = B − A + D − A ,

which can be written as

F = F 1 + F 2 = 2 ( B + D 2 − A ) = 2 ( E − A ) ,

where E is the midpoint of the segment BD that joins the points B and D.

Thus, the sum of the forces F₁ and F₂ is twice the segment joining A to the midpoint E of the segment joining the endpoints B and D of the two forces. The doubling of this length is easily achieved by defining a segments BC and DC parallel to AD and AB, respectively, to complete the parallelogram ABCD. The diagonal AC of this parallelogram is the sum of the two force vectors. This is known as the parallelogram rule for the addition of forces.

Point forces

When a force acts on a particle, it is applied to a single point (the particle volume is negligible): this is a point force and the particle is its application point. But an external force on an extended body (object) can be applied to a number of its constituent particles, i.e. can be "spread" over some volume or surface of the body. However, in order to determine its rotational effect on the body, it is necessary to specify its point of application (actually, the line of application, as explained below). The problem is usually resolved in the following ways:

Often the volume or surface on which the force acts is relatively small compared to the size of the body, so that it can be approximated by a point. It is usually not difficult to determine whether the error caused by such approximation is acceptable.

If it is not acceptable (obviously e.g. in the case of gravitational force), such "volume/surface" force should be described as a system of forces (components), each acting on a single particle, and then the calculation should be done for each of them separately. Such a calculation is typically simplified by the use of differential elements of the body volume/surface, and the integral calculus. In a number of cases, though, it can be shown that such a system of forces may be replaced by a single point force without the actual calculation (as in the case of uniform gravitational force).

In any case, the analysis of the rigid body motion begins with the point force model. And when a force acting on a body is shown graphically, the oriented line segment representing the force is usually drawn so as to "begin" (or "end") at the application point.

Rigid bodies

In the example shown in the diagram opposite, a single force F → acts at the application point H on a free rigid body. The body has the mass m and its center of mass is the point C. In the constant mass approximation, the force causes changes in the body motion described by the following expressions:

a → = F → m    is the center of mass acceleration; and α → = τ → I    is the angular acceleration of the body.

In the second expression, τ → is the torque or moment of force, whereas I is the moment of inertia of the body. A torque caused by a force F → is a vector quantity defined with respect to some reference point:

τ → = r → × F →    is the torque vector, and   τ = F k    is the amount of torque.

The vector r → is the position vector of the force application point, and in this example it is drawn from the center of mass as the reference point of(see diagram). The straight line segment k is the lever arm of the force F → with respect to the center of mass. As the illustration suggests, the torque does not change (the same lever arm) if the application point is moved along the line of the application of the force (dotted black line). More formally, this follows from the properties of the vector product, and shows that rotational effect of the force depends only on the position of its line of application, and not on the particular choice of the point of application along that line.

The torque vector is perpendicular to the plane defined by the force and the vector r → , and in this example it is directed towards the observer; the angular acceleration vector has the same direction. The right hand rule relates this direction to the clockwise or counter-clockwise rotation in the plane of the drawing.

The moment of inertia I is calculated with respect to the axis through the center of mass that is parallel with the torque. If the body shown in the illustration is a homogeneous disc, this moment of inertia is I = m r 2 / 2 . If the disc has the mass 0,5 kg and the radius 0,8 m, the moment of inertia is 0,16 kgm². If the amount of force is 2 N, and the lever arm 0,6 m, the amount of torque is 1,2 Nm. At the instant shown, the force gives to the disc the angular acceleration α = τ/I = 7,5 rad/s², and to its center of mass it gives the linear acceleration a = F/m = 4 m/s².

Resultant force

Resultant force and torque replaces the effects of a system of forces acting on the movement of a rigid body. An interesting special case is a torque-free resultant which can be found as follows:

1. Vector addition is used to find the net force;
2. Use the equation to determine the point of application with zero torque:

r → × F → R = ∑ i = 1 N ( r → i × F → i )

where F → R is the net force, r → locates its application point, and individual forces are F → i with application points r → i . It may be that there is no point of application that yields a torque-free resultant.

The diagram opposite illustrates simple graphical methods for finding the line of application of the resultant force of simple planar systems:

1. Lines of application of the actual forces F → 1 and F → 2 on the leftmost illustration intersect. After vector addition is performed "at the location of F → 1 ", the net force obtained is translated so that its line of application passes through the common intersection point. With respect to that point all torques are zero, so the torque of the resultant force F → R is equal to the sum of the torques of the actual forces.
2. The illustration in the middle of the diagram shows two parallel actual forces. After vector addition "at the location of F → 2 ", the net force is translated to the appropriate line of application, where it becomes the resultant force F → R . The procedure is based on decomposition of all forces into components for which the lines of application (pale dotted lines) intersect at one point (the so-called pole, arbitrarily set at the right side of the illustration). Then the arguments from the previous case are applied to the forces and their components to demonstrate the torque relationships.
3. The rightmost illustration shows a couple, two equal but opposite forces for which the amount of the net force is zero, but they produce the net torque τ = F d    where   d   is the distance between their lines of application. Since there is no resultant force, this torque can be [is?] described as "pure" torque.

Usage

In general, a system of forces acting on a rigid body can always be replaced by one force plus one pure (see previous section) torque. The force is the net force, but in order to calculate the additional torque, the net force must be assigned the line of action. The line of action can be selected arbitrarily, but the additional pure torque will depend on this choice. In a special case it is possible to find such line of action that this additional torque is zero.

The resultant force and torque can be determined for any configuration of forces. However, an interesting special case is a torque-free resultant which it is useful both conceptually and practically, because the body moves without rotating as if it was a particle.

Some authors do not distinguish the resultant force from the net force and use the terms as synonyms.