Puneet Varma (Editor)

Neo Hookean solid

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Neo-Hookean solid

A neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, the stress-strain curve of a neo-Hookean material is not linear. Instead, the relationship between applied stress and strain is initially linear, but at a certain point the stress-strain curve will plateau. The neo-Hookean model does not account for the dissipative release of energy as heat while straining the material and perfect elasticity is assumed at all stages of deformation.

Contents

The neo-Hookean model is based on the statistical thermodynamics of cross-linked polymer chains and is usable for plastics and rubber-like substances. Cross-linked polymers will act in a neo-Hookean manner because initially the polymer chains can move relative to each other when a stress is applied. However, at a certain point the polymer chains will be stretched to the maximum point that the covalent cross links will allow, and this will cause a dramatic increase in the elastic modulus of the material. The neo-Hookean material model does not predict that increase in modulus at large strains and is typically accurate only for strains less than 20%. The model is also inadequate for biaxial states of stress and has been superseded by the Mooney-Rivlin model.

The strain energy density function for an incompressible neo-Hookean material in a three-dimensional description is

W = C 1 ( I 1 − 3 )

where C 1 is a material constant, and I 1 is the first invariant of the right Cauchy-Green deformation tensor, i.e.,

I 1 = λ 1 2 + λ 2 2 + λ 3 2  

where λ i are the principal stretches. For a compressible neo-Hookean material the strain energy density function is given by

W = C 1   ( I ¯ 1 − 3 ) + D 1   ( J − 1 ) 2   ;     J = det ( F ) = λ 1 λ 2 λ 3

where D 1 is a material constant, I ¯ 1 = J − 2 / 3 I 1 is the first invariant of the isochoric part of the right Cauchy-Green deformation tensor, and F is the deformation gradient. It can be shown that in 2D, the strain energy density function is

W = C 1   ( I ¯ 1 − 2 ) + D 1   ( J − 1 ) 2   ;

where, in this case, I ¯ 1 = J − 1 I 1 .

Several alternative formulations exist for compressible neo-Hookean materials, for example

W = C 1   ( I 1 − 3 − 2 ln ⁡ J ) + D 1   ( ln ⁡ J ) 2

For consistency with linear elasticity,

C 1 = μ 2   ;     D 1 = κ 2

where μ is the shear modulus and κ is the bulk modulus.

Compressible neo-Hookean material

For a compressible Rivlin neo-Hookean material the Cauchy stress is given by

J   σ = − p   1 + 2 C 1   d e v ( B ¯ ) = − p   1 + 2 C 1 J 2 / 3   d e v ( B )

where B is the left Cauchy-Green deformation tensor, and

p := − 2 D 1   J ( J − 1 )   ;     d e v ( B ¯ ) = B ¯ − 1 3 I ¯ 1 1   ;     B ¯ = J − 2 / 3 B   .

For infinitesimal strains ( ε )

J ≈ 1 + t r ( ε )   ;     B ≈ 1 + 2 ε

and the Cauchy stress can be expressed as

σ ≈ 4 C 1 ( ε − 1 3 t r ( ε ) 1 ) + 2 D 1 t r ( ε ) 1

Comparison with Hooke's law shows that μ = 2 C 1 and κ = 2 D 1 .

Incompressible neo-Hookean material

For an incompressible neo-Hookean material with J = 1

σ = − p   1 + 2 C 1 B

where p is an undetermined pressure.

Compressible neo-Hookean material

For a compressible neo-Hookean hyperelastic material, the principal components of the Cauchy stress are given by

σ i = 2 C 1 J − 5 / 3 [ λ i 2 − I 1 3 ] + 2 D 1 ( J − 1 )   ;     i = 1 , 2 , 3

Therefore, the differences between the principal stresses are

σ 11 − σ 33 = 2 C 1 J 5 / 3 ( λ 1 2 − λ 3 2 )   ;     σ 22 − σ 33 = 2 C 1 J 5 / 3 ( λ 2 2 − λ 3 2 )

Incompressible neo-Hookean material

In terms of the principal stretches, the Cauchy stress differences for an incompressible hyperelastic material are given by

σ 11 − σ 33 = λ 1   ∂ W ∂ λ 1 − λ 3   ∂ W ∂ λ 3   ;     σ 22 − σ 33 = λ 2   ∂ W ∂ λ 2 − λ 3   ∂ W ∂ λ 3

For an incompressible neo-Hookean material,

W = C 1 ( λ 1 2 + λ 2 2 + λ 3 2 − 3 )   ;     λ 1 λ 2 λ 3 = 1

Therefore,

∂ W ∂ λ 1 = 2 C 1 λ 1   ;     ∂ W ∂ λ 2 = 2 C 1 λ 2   ;     ∂ W ∂ λ 3 = 2 C 1 λ 3

which gives

σ 11 − σ 33 = 2 ( λ 1 2 − λ 3 2 ) C 1   ;     σ 22 − σ 33 = 2 ( λ 2 2 − λ 3 2 ) C 1

Compressible neo-Hookean material

For a compressible material undergoing uniaxial extension, the principal stretches are

λ 1 = λ   ;     λ 2 = λ 3 = J λ   ;     I 1 = λ 2 + 2 J λ

Hence, the true (Cauchy) stresses for a compressible neo-Hookean material are given by

σ 11 = 4 C 1 3 J 5 / 3 ( λ 2 − J λ ) + 2 D 1 ( J − 1 ) σ 22 = σ 33 = 2 C 1 3 J 5 / 3 ( J λ − λ 2 ) + 2 D 1 ( J − 1 )

The stress differences are given by

σ 11 − σ 33 = 2 C 1 J 5 / 3 ( λ 2 − J λ )   ;     σ 22 − σ 33 = 0

If the material is unconstrained we have σ 22 = σ 33 = 0 . Then

σ 11 = 2 C 1 J 5 / 3 ( λ 2 − J λ )

Equating the two expressions for σ 11 gives a relation for J as a function of λ , i.e.,

4 C 1 3 J 5 / 3 ( λ 2 − J λ ) + 2 D 1 ( J − 1 ) = 2 C 1 J 5 / 3 ( λ 2 − J λ )

or

D 1 J 8 / 3 − D 1 J 5 / 3 + C 1 3 λ J − C 1 λ 2 3 = 0

The above equation can be solved numerically using a Newton-Raphson iterative root finding procedure.

Incompressible neo-Hookean material

Under uniaxial extension, λ 1 = λ and λ 2 = λ 3 = 1 / λ . Therefore,

σ 11 − σ 33 = 2 C 1 ( λ 2 − 1 λ )   ;     σ 22 − σ 33 = 0

Assuming no traction on the sides, σ 22 = σ 33 = 0 , so we can write

σ 11 = 2 C 1 ( λ 2 − 1 λ ) = 2 C 1 ( 3 ε 11 + 3 ε 11 2 + ε 11 3 1 + ε 11 )

where ε 11 = λ − 1 is the engineering strain. This equation is often written in alternative notation as

T 11 = 2 C 1 ( α 2 − 1 α )

The equation above is for the true stress (ratio of the elongation force to deformed cross-section). For the engineering stress the equation is:

σ 11 e n g = 2 C 1 ( λ − 1 λ 2 )

For small deformations ε ≪ 1 we will have:

σ 11 = 6 C 1 ε = 3 μ ε

Thus, the equivalent Young's modulus of a neo-Hookean solid in uniaxial extension is 3 μ , which is in concordance with linear elasticity ( E = 2 μ ( 1 + ν ) with ν = 0.5 for incompressibility).

Compressible neo-Hookean material

In the case of equibiaxial extension

λ 1 = λ 2 = λ   ;     λ 3 = J λ 2   ;     I 1 = 2 λ 2 + J 2 λ 4

Therefore,

σ 11 = 2 C 1 [ λ 2 J 5 / 3 − 1 3 J ( 2 λ 2 + J 2 λ 4 ) ] + 2 D 1 ( J − 1 ) = σ 22 σ 33 = 2 C 1 [ J 1 / 3 λ 4 − 1 3 J ( 2 λ 2 + J 2 λ 4 ) ] + 2 D 1 ( J − 1 )

The stress differences are

σ 11 − σ 22 = 0   ;     σ 11 − σ 33 = 2 C 1 J 5 / 3 ( λ 2 − J 2 λ 4 )

If the material is in a state of plane stress then σ 33 = 0 and we have

σ 11 = σ 22 = 2 C 1 J 5 / 3 ( λ 2 − J 2 λ 4 )

We also have a relation between J and λ :

2 C 1 [ λ 2 J 5 / 3 − 1 3 J ( 2 λ 2 + J 2 λ 4 ) ] + 2 D 1 ( J − 1 ) = 2 C 1 J 5 / 3 ( λ 2 − J 2 λ 4 )

or,

( 2 D 1 − C 1 λ 4 ) J 2 + 3 C 1 λ 4 J 4 / 3 − 3 D 1 J − 2 C 1 λ 2 = 0

This equation can be solved for J using Newton's method.

Incompressible neo-Hookean material

For an incompressible material J = 1 and the differences between the principal Cauchy stresses take the form

σ 11 − σ 22 = 0   ;     σ 11 − σ 33 = 2 C 1 ( λ 2 − 1 λ 4 )

Under plane stress conditions we have

σ 11 = 2 C 1 ( λ 2 − 1 λ 4 )

Pure dilation

For the case of pure dilation

λ 1 = λ 2 = λ 3 = λ   :     J = λ 3   ;     I 1 = 3 λ 2

Therefore, the principal Cauchy stresses for a compressible neo-Hookean material are given by

σ i = 2 C 1 ( 1 λ 3 − 1 λ ) + 2 D 1 ( λ 3 − 1 )

If the material is incompressible then λ 3 = 1 and the principal stresses can be arbitrary.

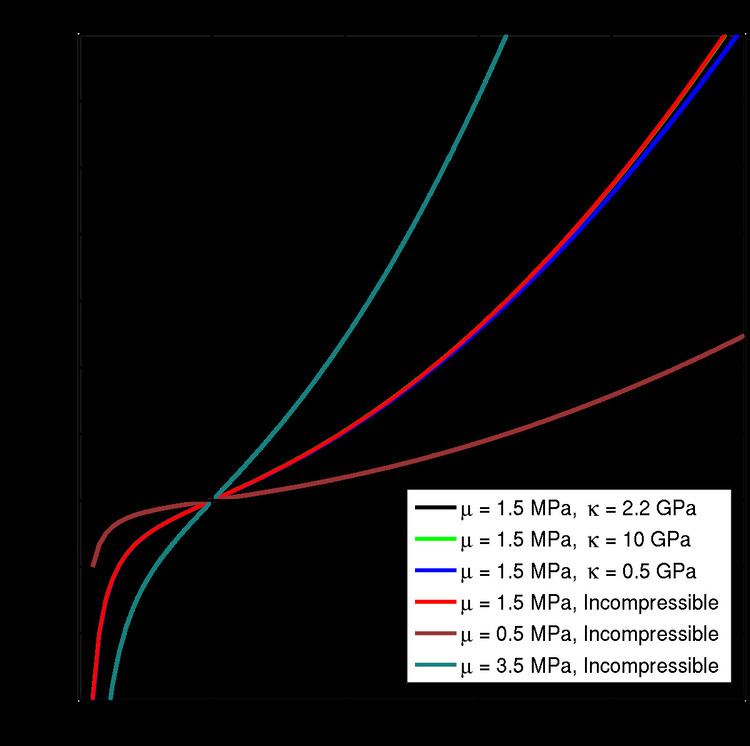
The figures below show that extremely high stresses are needed to achieve large triaxial extensions or compressions. Equivalently, relatively small triaxial stretch states can cause very high stresses to develop in a rubber-like material. Note also that the magnitude of the stress is quite sensitive to the bulk modulus but not to the shear modulus.

Simple shear

For the case of simple shear the deformation gradient in terms of components with respect to a reference basis is of the form

F = [ 1 γ 0 0 1 0 0 0 1 ]

where γ is the shear deformation. Therefore the left Cauchy-Green deformation tensor is

B = F ⋅ F T = [ 1 + γ 2 γ 0 γ 1 0 0 0 1 ]

Compressible neo-Hookean material

In this case J = det ( F ) = 1 . Hence, σ = 2 C 1 d e v ( B ) . Now,

d e v ( B ) = B − 1 3 t r ( B ) 1 = B − 1 3 ( 3 + γ 2 ) 1 = [ 2 3 γ 2 γ 0 γ − 1 3 γ 2 0 0 0 − 1 3 γ 2 ]

Hence the Cauchy stress is given by

σ = [ 4 C 1 3 γ 2 2 C 1 γ 0 2 C 1 γ − 2 C 1 3 γ 2 0 0 − 2 C 1 3 γ 2 ]

Incompressible neo-Hookean material

Using the relation for the Cauchy stress for an incompressible neo-Hookean material we get

σ = − p 1 + 2 C 1 B = [ 2 C 1 ( 1 + γ 2 ) − p 2 C 1 γ 0 2 C 1 γ 2 C 1 − p 0 0 0 2 C 1 − p ]

Thus neo-Hookean solid shows linear dependence of shear stresses upon shear deformation and quadratic dependence of the normal stress difference on the shear deformation. Note that the expressions for the Cauchy stress for a compressible and an incompressible neo-Hookean material in simple shear represent the same quantity and provide a means of determining the unknown pressure p .

References

Neo-Hookean solid Wikipedia
(Text) CC BY-SA