Negative frequency

Sinusoids

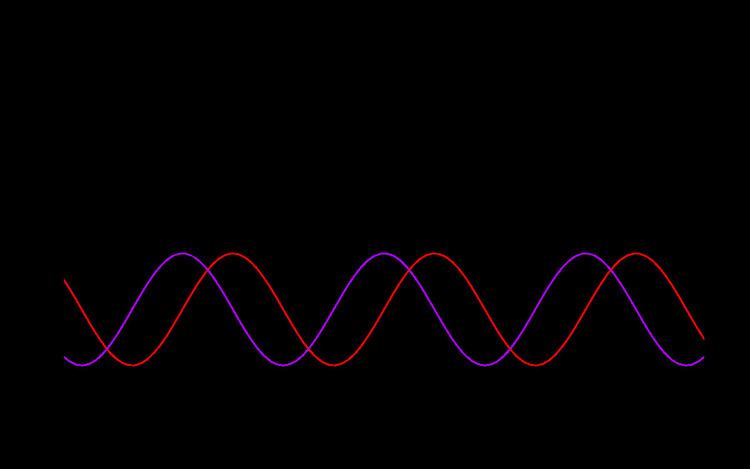
Let ω be a nonnegative parameter with units of radians/sec. Then the angular function (angle vs. time) −ωt + θ, has slope −ω, which is called a negative frequency. But when the function is used as the argument of a cosine operator, the result is indistinguishable from cos(ωt − θ).  Similarly, sin(−ωt + θ) is indistinguishable from sin(ωt − θ + π). Thus any sinusoids can be represented in terms of positive frequencies. The sign of the underlying phase slope is ambiguous.

The ambiguity is resolved when the cosine and sine operators can be observed simultaneously, because cos(ωt + θ) leads sin(ωt + θ) by 1/4 cycle (= π/2 radians) when ω > 0, and lags by 1/4 cycle when ω < 0.  Similarly, a vector, (cos t, sin t), rotates counter-clockwise at 1 radian/sec, and completes a circle every 2π seconds, and the vector (cos -t, sin -t) rotates in the other direction.

The sign of ω is also preserved in the complex-valued function:

since R(t) and I(t) can be separately extracted and compared. Although e i ω t   clearly contains more information than either of its components, a common interpretation is that it is a simpler function, because:

which gives rise to the interpretation that cos(ωt) comprises both positive and negative frequencies.  But the sum is actually a cancellation that contains less, not more, information. Any measure that indicates both frequencies includes a false positive, because ω can have only one sign.  The Fourier transform, for instance, merely tells us that cos(ωt) correlates equally well with both cos(ωt) + i sin(ωt) and with cos(ωt) − i sin(ωt).

Applications

Perhaps the most well-known application of negative frequency is the calculation:

which is a measure of the amount of frequency ω in the function x(t) over the interval (a, b). When evaluated as a continuous function of ω for the theoretical interval (−∞, ∞), it is known as the Fourier transform of x(t). A brief explanation is that the product of two complex sinusoids is also a complex sinusoid whose frequency is the sum of the original frequencies. So when ω is positive, e − i ω t causes all the frequencies of x(t) to be reduced by amount ω. Whatever part of x(t) that was at frequency ω is changed to frequency zero, which is just a constant whose amplitude level is a measure of the strength of the original ω content. And whatever part of x(t) that was at frequency zero is changed to a sinusoid at frequency −ω. Similarly, all other frequencies are changed to non-zero values. As the interval (a, b) increases, the contribution of the constant term grows in proportion. But the contributions of the sinusoidal terms only oscillate around zero. So X(ω) improves as a relative measure of the amount of frequency ω in the function x(t).

The Fourier transform of   e i ω t   produces a non-zero response only at frequency ω. The transform of cos ⁡ ( ω t ) has responses at both ω and −ω, as anticipated by Eq.2.