 | ||
Multidimensional modulation (MD modulation) is modifying or multiplying an MD signal (typically sinusoidal and referred to as the carrier signal) with another signal that carries some information or message. In the frequency domain, the signal is moved from one frequency to another.
Contents
- BackgroundMotivation
- MD Fourier Transform FT
- Computation
- Multidimensional AM and FM
- 2 D Modulation based Applications
- 2 D AM and FM analysis
- 3 D Modulation based Applications
- References
if
then
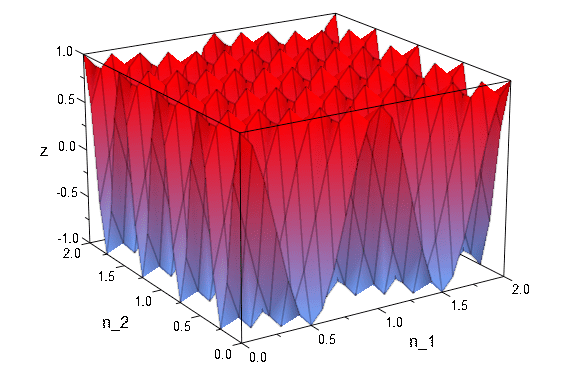
Typically the carrier signal is a sinusoidal signal and in various applications. The figures below illustrate a quick example of a 2-D modulation. The original signal from (3) is modulated with a sinusoidal signal to get (4). The equations (5) and (6) are the real and the imaginary components of the modulated signal.
Background/Motivation
The MD modulation is one of the properties of the Multidimensional Fourier Transform.
MD Fourier Transform (FT)
Fourier Transform (FT) of multi-dimensional (MD) signal or system is the transform of the MD signal or system that decomposes it into its frequency components. Essentially, it's the frequency response of the MD signal or system, so it depicts the frequency characteristics of the signal or system. A special case of the MD transform is the 1-D Fourier transform.
Computation
The formula for computing the Fourier transform of an MD signal is
If the frequency response is given instead, then the inverse FT formula is used to derive the input signal or system. In this case the formula used is:
Multidimensional AM and FM
Multidimensional AM or FM is AM-FM modulation where the a Multidimensional message signal is modulated (or multiplied) with a Multidimensional sinusoidal signal. From the special case of Parseval’s theorem (MD FT Properties), it is noted that the energy or power of a signal is directly proportional to the magnitude of the signal, and since most of the signals in this case are sinusoidal, it is well noted that the energy or power is directly proportional to the amplitude of the sinusoid. Since power management is always an issue, the modulation of the amplitude isn’t always the best solution when the application is trying to be power conscious.
2-D Modulation based Applications
A 2-D modulation comprises a space domain that has 2 independent variables e.g. x(n1,n2) with a corresponding frequency domain that also has 2 independent variables X(ω1, ω2).
2-D AM and FM analysis
Image texturization is an application of multidimensional AM-FM modulation. In this method, the image (2-D signal) is expressed into its special frequencies and amplitude estimates. The signal is represented as a product of 2 FM functions (using the independent frequencies), making is separable. Using the instantaneous frequency, the image can be represented topologically to illustrate its texture.
3-D Modulation based Applications
3-D modulation uses 3-D message and carrier signals.
3D scanner: Some 3-D scanners used modulated light, typically amplitude modulation, together with a camera to scan an object.
3-D TOF cameras: They use modulated light sources and it’s reflection for depth perception computation. In essence, creating a 2-D image with depth perception helps separate the foreground and background.
