Multicritical point

Definition

The union of all the points of the parameter space for which the system is critical is called a critical manifold.

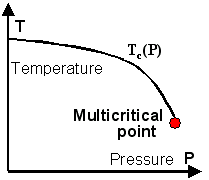
As an example consider a substance ferromagnetic below a transition temperature T c , and paramagnetic above T c . The parameter space here is the temperature axis, and the critical manifold consists of the point T c . Now add hydrostatic pressure P to the parameter space. Under hydrostatic pressure the substance normally still becomes ferromagnetic below a temperature T c ( P ).

This leads to a critical curve in the ( T , P ) plane - a 1 -dimensional critical manifold. Also taking into account shear stress K as a thermodynamic parameter leads to a critical surface T c ( P , K ) in the ( T , P , K ) parameter space - a 2 -dimensional critical manifold. Critical manifolds of dimension d > 1 and d > 2 may have physically reachable borders of dimension d − 1 which in turn may have borders of dimension d − 2 . The system still is critical at these borders. However, criticality terminates for good reason, and the points on the borders normally belong to another universality class than the universality class realized within the critical manifold. All the points on the border of a critical manifold are multicritical points. Instead of terminating somewhere critical manifolds also may branch or intersect. The points on the intersections or branch lines also are multicritical points.

At least two parameters must be adjusted to reach a multicritical point. A 2 -dimensional critical manifold may have two 1 -dimensional borders intersecting at a point. Two parameters must be adjusted to reach such a border, three parameters must be adjusted to reach the intersection of the two borders. A system of this type represents up to four universality classes: one within the critical manifold, two on the borders and one on the intersection of the borders.

The gas-liquid critical point is not multicritical, because the phase transition at the vapour pressure curve P ( T ) is discontinuous and the critical manifold thus consists of a single point.

Tricritical Point and Multicritical Points of Higher Order

To reach a tricritical point the parameters must be tuned in such a way that the renormalized counterpart of the ϕ 4 -term of the Hamiltonian vanishes. A well-known experimental realization is found in the mixture of Helium-3 and Helium-4.

Lifshitz Point

To reach a Lifshitz point the parameters must be tuned in such a way that the renormalized counterpart of the ( ∇ ϕ ) 2 -term of the Hamiltonian vanishes. Consequently, at the Lifshitz point phases of uniform and modulated order meet the disordered phase. An experimental example is the magnet MnP. A Lifshitz point is realized in a prototypical way in the ANNNI model.

Lifshitz Tricritical Point

This multicritical point is simultaneously tricritical and Lifshitz. Three parameters must be adjusted to reach a Lifshitz tricritical point. Such a point has been discussed to occur in non-stoichiometric ferroelectrics.

Renormalization Group

The renormalization group provides a detailed and quantitative explanation of critical phenomena.