Supriya Ghosh (Editor)

Moore plane

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Moore plane

In mathematics, the Moore plane, also sometimes called Niemytzki plane (or Nemytskii plane, Nemytskii's tangent disk topology), is a topological space. It is a completely regular Hausdorff space (also called Tychonoff space) that is not normal. It is named after Robert Lee Moore and Viktor Vladimirovich Nemytskii.

Contents

Definition

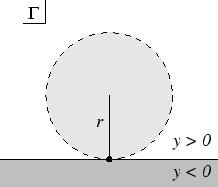
If Γ is the (closed) upper half-plane Γ = { ( x , y ) ∈ R 2 | y ≥ 0 } , then a topology may be defined on Γ by taking a local basis B ( p , q ) as follows:

  • Elements of the local basis at points ( x , y ) with y > 0 are the open discs in the plane which are small enough to lie within Γ . Thus the subspace topology inherited by Γ ∖ { ( x , 0 ) | x ∈ R } is the same as the subspace topology inherited from the standard topology of the Euclidean plane.
  • Elements of the local basis at points p = ( x , 0 ) are sets { p } ∪ A where A is an open disc in the upper half-plane which is tangent to the x axis at p.

    • That is, the local basis is given by

    B ( p , q ) = { { U ϵ ( p , q ) := { ( x , y ) : ( x − p ) 2 + ( y − q ) 2 < ϵ 2 } ∣ ϵ > 0 } , if  q > 0 ; { V ϵ ( p ) := { ( p , 0 ) } ∪ { ( x , y ) : ( x − p ) 2 + ( y − ϵ ) 2 < ϵ 2 } ∣ ϵ > 0 } , if  q = 0.

    Properties

  • The Moore plane Γ is separable, that is, it has a countable dense subset.
  • The Moore plane is a completely regular Hausdorff space (i.e. Tychonoff space), which is not normal.
  • The subspace { ( x , 0 ) ∈ Γ | x ∈ R } of Γ has, as its subspace topology, the discrete topology. Thus, the Moore plane shows that a subspace of a separable space need not be separable.
  • The Moore plane is first countable, but not second countable or Lindelöf.
  • The Moore plane is not locally compact.
  • The Moore plane is countably metacompact but not metacompact.

    • Proof that the Moore plane is not normal

    The fact that this space M is not normal can be established by the following counting argument (which is very similar to the argument that the Sorgenfrey plane is not normal):

    1. On the one hand, the countable set S := { ( p , q ) ∈ Q × Q : q > 0 } of points with rational coordinates is dense in M; hence every continuous function f : M → R is determined by its restriction to S , so there can be at most | R | | S | = 2 ℵ 0 many continuous real-valued functions on M.
    2. On the other hand, the real line L := { ( p , 0 ) : p ∈ R } is a closed discrete subspace of M with 2 ℵ 0 many points. So there are 2 2 ℵ 0 > 2 ℵ 0 many continuous functions from L to R . Not all these functions can be extended to continuous functions on M.
    3. Hence M is not normal, because by the Tietze extension theorem all continuous functions defined on a closed subspace of a normal space can be extended to a continuous function on the whole space.

    In fact, if X is a separable topological space having an uncountable closed discrete subspace, X cannot be normal.

    References

    Moore plane Wikipedia
    (Text) CC BY-SA