 | ||
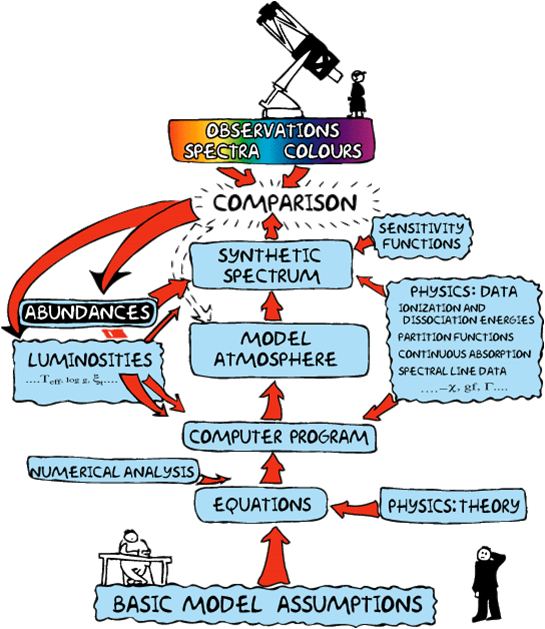
The photosphere denotes those solar or stellar surface layers from which optical radiation escapes. These stellar outer layers can be modeled by different computer programs. Often, calculated models are used, together with other programs, to calculate synthetic spectra for stars. For example, in varying the assumed abundance of a chemical element, and comparing the synthetic spectra to observed ones, the abundance of that element in that particular star can be determined. As computers have evolved, the complexity of the models has deepened, becoming more realistic in including more physical data and excluding more of the simplifying assumptions. This evolution of the models has also made them applicable to different kinds of stars.
Contents
- Local Thermodynamic Equilibrium LTE
- Plane parallel and spherical atmospheres
- Expanding atmospheres
- Hydrostatic equilibrium
- Mixing length and microturbulence
- Different methods of treating opacity
- Different models
- ATLAS
- MARCS
- PHOENIX
- PoWR
- 3D hydrodynamical models
- Applications of Model Photospheres
- Stellar Evolution
- Synthetic Spectra
- References
Local Thermodynamic Equilibrium (LTE)
This assumption (LTE) means that within any local computational volume, the state of thermodynamical equilibrium is assumed:
Plane parallel and spherical atmospheres
A common simplifying assumption is that the atmosphere is plane parallel, meaning that physical variables depend on one space coordinate only: the vertical depth (i.e., one assumes that we see the stellar atmosphere "head-on", ignoring the curved portions towards the limbs). In stars where the photosphere is relatively thick compared to the stellar diameter, this is not a good approximation and an assumption of a spherical atmosphere is more appropriate.
Expanding atmospheres
Many stars lose mass in the form of a stellar wind. Especially for stars which are very hot (photospheric temperatures > 10,000 Kelvin) and very luminous, these winds can be so dense that major parts of the emergent spectrum are formed in an "expanding atmosphere", i.e. in layers that are moving outward with a high speed that can reach a few 1000 km/s.
Hydrostatic equilibrium
This means that the star is currently not undergoing any radical changes in structure involving large scale pulsations, flows or mass loss.
Mixing length and microturbulence
This assumption means that the convective motions in the atmosphere are described by the mixing-length theory, modeled as parcels of gas rising and disintegrating. To account for some of the small-scale effects in convective motions, a parameter called microturbulence is often used. The microturbulence corresponds to the motions of atoms or molecules on scales smaller than the photon mean free path.
Different methods of treating opacity
To fully model the photosphere one would need to include every absorption line of every element present. This is not feasible because it would be computationally extremely demanding, and also all spectra are not fully known. Therefore one needs to simplify the treatment of opacity. Methods used in photospheric models include:
Opacity sampling means that the radiative transfer is evaluated for a number of optical wavelengths spread across the interesting parts of the spectrum. Although the model would improve with more frequencies included, opacity sampling uses as few as practical, to still get a realistic model, thereby minimizing calculation time.
In using opacity distribution functions, the spectra are divided into subsections, within which the absorption probabilities are rearranged and simplified to one smooth function. Similar to the opacity sampling method, this is improved by adding more intervals but at the cost of prolonging the computation time.
Different models
There are several different computer codes available modeling stellar photospheres. Some of them are described here and some of them are linked under "External links" below.
ATLAS
The ATLAS code was originally presented in 1970 by Robert Kurucz using the assumption of LTE and hydrostatic and plane parallel atmospheres. Since the source code is publicly available on the web, it has been amended by different persons numerous times over the years and nowadays exists in many versions. There are both plane parallel and spherical versions as well as those using opacity sampling or opacity distribution functions.
MARCS
The MARCS (Model Atmospheres in Radiative and Convective Scheme) code was originally presented in 1975 by Bengt Gustafsson, Roger Bell and others. The original code simulated stellar spectra assuming the atmosphere to be in hydrostatic equilibrium, plane parallel, with convection described by mixing-length theory. The evolution of the code has since involved better modeling of the line opacity (opacity sampling instead of opacity distribution functions), spherical modeling and including an increasing number of physical data. Nowadays a large grid of different models is available on the web.
PHOENIX
The PHOENIX code is "risen from the ashes" of an earlier code called SNIRIS and mainly developed by Peter Hauschildt (Hamburger Sternwarte) from 1992 onwards; it is regularly updated and made available on the web It runs in two different spatial configuration modes: the "classic" one-dimensional mode, assuming spherical symmetry, and the three-dimensional mode. It allows for calculations for many different astrophysical objects, i.e. supernovae, novae, stars and planets. It considers scattering and dust and allows for non-LTE computations over many atomic species, plus LTE over atoms and molecules.
PoWR
The PoWR (Potsdam Wolf-Rayet) code is designed for expanding stellar atmospheres, i.e. for stars with a stellar wind. It has been developed since the 1990s by Wolf-Rainer Hamann and collaborators at the Universität Potsdam (Germany) especially for simulating Wolf-Rayet stars, which are hot stars with very strong mass loss. Adopting spherical symmetry and stationarity, the program computes the occupation numbers of the atomic energy states, including the ionization balance, in non-LTE, and consistently solves the radiative transfer problem in the comoving frame. The stellar wind parameters (mass-loss rate, wind speed) can be specified as free parameter, or, alternatively, calculated from the hydrodynamic equation consistently. As the PoWR code treats consistently the static and expanding layers of the stellar atmosphere, it is applicable for any types of hot stars. The code as such is not yet public, but large sets of models for Wolf-Rayet stars are available on the web.
3D hydrodynamical models
There are efforts to construct models not assuming LTE, and/or computing the detailed hydrodynamic motions instead of hydrostatic assumptions. These models are physically more realistic but also require more physical data such as cross sections and probabilities for different atomic processes. Such models are computationally rather demanding, and have not yet reached a stage of broader distribution.
Applications of Model Photospheres
Model Atmospheres, while interesting in their own right, are frequently used as part of input recipes and tools for studying other astrophysical problems.
Stellar Evolution
As a result of stellar evolution, changes in the internal structure of stars manifest themselves in the photosphere.
Synthetic Spectra
Spectral synthesis programs (e.g. Moog (code)) often use previously generated model photospheres to describe the physical conditions (temperature, pressure, etc...) through which photons must travel to escape the stellar atmosphere. Together with a list of absorption lines and an elemental abundance table, spectral synthesis programs generate synthetic spectra. By comparing these synthetic spectra to observed spectra of distant stars, astronomers can determine the properties (temperature, age, chemical composition, etc...) of these stars.
