Harman Patil (Editor)

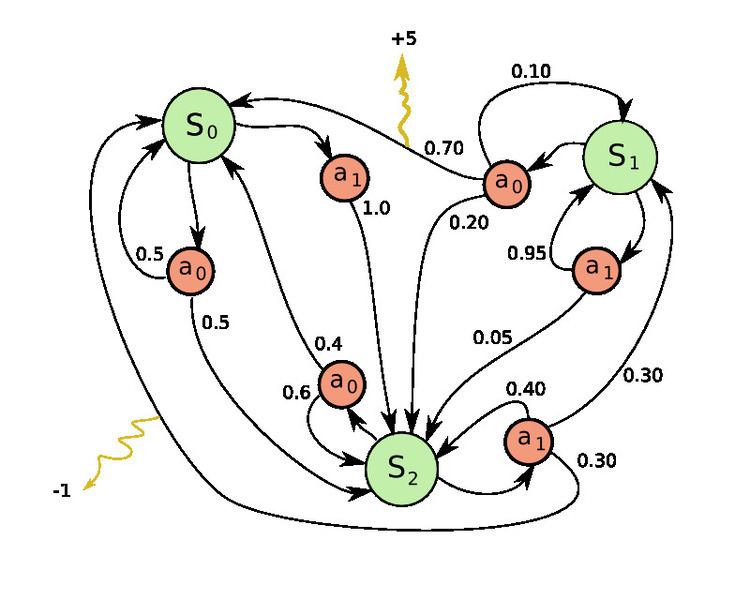
Markov decision process

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Markov decision process

Markov decision processes (MDPs) provide a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via dynamic programming and reinforcement learning. MDPs were known at least as early as the 1950s (cf. Bellman 1957). A core body of research on Markov decision processes resulted from Ronald A. Howard's book published in 1960, Dynamic Programming and Markov Processes. They are used in a wide area of disciplines, including robotics, automated control, economics, and manufacturing.

Contents

More precisely, a Markov Decision Process is a discrete time stochastic control process. At each time step, the process is in some state s , and the decision maker may choose any action a that is available in state s . The process responds at the next time step by randomly moving into a new state s ′ , and giving the decision maker a corresponding reward R a ( s , s ′ ) .

The probability that the process moves into its new state s ′ is influenced by the chosen action. Specifically, it is given by the state transition function P a ( s , s ′ ) . Thus, the next state s ′ depends on the current state s and the decision maker's action a . But given s and a , it is conditionally independent of all previous states and actions; in other words, the state transitions of an MDP satisfies the Markov property.

Markov decision processes are an extension of Markov chains; the difference is the addition of actions (allowing choice) and rewards (giving motivation). Conversely, if only one action exists for each state (e.g. "wait") and all rewards are the same (e.g. "zero"), a Markov decision process reduces to a Markov chain.

Definition

A Markov decision process is a 5-tuple ( S , A , P ⋅ ( ⋅ , ⋅ ) , R ⋅ ( ⋅ , ⋅ ) , γ ) , where

  • S is a finite set of states,
  • A is a finite set of actions (alternatively, A s is the finite set of actions available from state s ),
  • P a ( s , s ′ ) = Pr ( s t + 1 = s ′ ∣ s t = s , a t = a ) is the probability that action a in state s at time t will lead to state s ′ at time t + 1 ,
  • R a ( s , s ′ ) is the immediate reward (or expected immediate reward) received after transitioning from state s to state s ′ , due to action a
  • γ ∈ [ 0 , 1 ] is the discount factor, which represents the difference in importance between future rewards and present rewards.

    • (Note: The theory of Markov decision processes does not state that S or A are finite, but the basic algorithms below assume that they are finite.)

    Problem

    The core problem of MDPs is to find a "policy" for the decision maker: a function π that specifies the action π ( s ) that the decision maker will choose when in state s . Note that once a Markov decision process is combined with a policy in this way, this fixes the action for each state and the resulting combination behaves like a Markov chain.

    The goal is to choose a policy π that will maximize some cumulative function of the random rewards, typically the expected discounted sum over a potentially infinite horizon:

    ∑ t = 0 ∞ γ t R a t ( s t , s t + 1 )    (where we choose a t = π ( s t ) )

    where   γ   is the discount factor and satisfies 0 ≤   γ   < 1 . (For example, γ = 1 / ( 1 + r ) when the discount rate is r.) γ is typically close to 1.

    Because of the Markov property, the optimal policy for this particular problem can indeed be written as a function of s only, as assumed above.

    Algorithms

    MDPs can be solved by linear programming or dynamic programming. In what follows we present the latter approach.

    Suppose we know the state transition function P and the reward function R , and we wish to calculate the policy that maximizes the expected discounted reward.

    The standard family of algorithms to calculate this optimal policy requires storage for two arrays indexed by state: value V , which contains real values, and policy π which contains actions. At the end of the algorithm, π will contain the solution and V ( s ) will contain the discounted sum of the rewards to be earned (on average) by following that solution from state s .

    The algorithm has the following two kinds of steps, which are repeated in some order for all the states until no further changes take place. They are defined recursively as follows:

    π ( s ) := arg ⁡ max a { ∑ s ′ P a ( s , s ′ ) ( R a ( s , s ′ ) + γ V ( s ′ ) ) } V ( s ) := ∑ s ′ P π ( s ) ( s , s ′ ) ( R π ( s ) ( s , s ′ ) + γ V ( s ′ ) )

    Their order depends on the variant of the algorithm; one can also do them for all states at once or state by state, and more often to some states than others. As long as no state is permanently excluded from either of the steps, the algorithm will eventually arrive at the correct solution.

    Value iteration

    In value iteration (Bellman 1957), which is also called backward induction, the π function is not used; instead, the value of π ( s ) is calculated within V ( s ) whenever it is needed. Lloyd Shapley's 1953 paper on stochastic games included as a special case the value iteration method for MDPs, but this was recognized only later on.

    Substituting the calculation of π ( s ) into the calculation of V ( s ) gives the combined step:

    V i + 1 ( s ) := max a { ∑ s ′ P a ( s , s ′ ) ( R a ( s , s ′ ) + γ V i ( s ′ ) ) } ,

    where i is the iteration number. Value iteration starts at i = 0 and V 0 as a guess of the value function. It then iterates, repeatedly computing V i + 1 for all states s , until V converges with the left-hand side equal to the right-hand side (which is the "Bellman equation" for this problem).

    Policy iteration

    In policy iteration (Howard 1960), step one is performed once, and then step two is repeated until it converges. Then step one is again performed once and so on.

    Instead of repeating step two to convergence, it may be formulated and solved as a set of linear equations.

    This variant has the advantage that there is a definite stopping condition: when the array π does not change in the course of applying step 1 to all states, the algorithm is completed.

    Modified policy iteration

    In modified policy iteration (van Nunen 1976; Puterman & Shin 1978), step one is performed once, and then step two is repeated several times. Then step one is again performed once and so on.

    Prioritized sweeping

    In this variant, the steps are preferentially applied to states which are in some way important - whether based on the algorithm (there were large changes in V or π around those states recently) or based on use (those states are near the starting state, or otherwise of interest to the person or program using the algorithm).

    Extensions and generalizations

    A Markov decision process is a stochastic game with only one player.

    Partial observability

    The solution above assumes that the state s is known when action is to be taken; otherwise π ( s ) cannot be calculated. When this assumption is not true, the problem is called a partially observable Markov decision process or POMDP.

    A major advance in this area was provided by Burnetas and Katehakis in "Optimal adaptive policies for Markov decision processes". In this work a class of adaptive policies that possess uniformly maximum convergence rate properties for the total expected finite horizon reward, were constructed under the assumptions of finite state-action spaces and irreducibility of the transition law. These policies prescribe that the choice of actions, at each state and time period, should be based on indices that are inflations of the right-hand side of the estimated average reward optimality equations.

    Reinforcement learning

    If the probabilities or rewards are unknown, the problem is one of reinforcement learning (Sutton & Barto 1998).

    For this purpose it is useful to define a further function, which corresponds to taking the action a and then continuing optimally (or according to whatever policy one currently has):

      Q ( s , a ) = ∑ s ′ P a ( s , s ′ ) ( R a ( s , s ′ ) + γ V ( s ′ ) ) .  

    While this function is also unknown, experience during learning is based on ( s , a ) pairs (together with the outcome s ′ ; that is, "I was in state s and I tried doing a and s ′ happened"). Thus, one has an array Q and uses experience to update it directly. This is known as Q‑learning.

    Reinforcement learning can solve Markov decision processes without explicit specification of the transition probabilities; the values of the transition probabilities are needed in value and policy iteration. In reinforcement learning, instead of explicit specification of the transition probabilities, the transition probabilities are accessed through a simulator that is typically restarted many times from a uniformly random initial state. Reinforcement learning can also be combined with function approximation to address problems with a very large number of states.

    Learning Automata

    Another application of MDP process in machine learning theory is called learning automata. This is also one type of reinforcement learning if the environment is in stochastic manner. The first detail learning automata paper is surveyed by Narendra and Thathachar (1974), which were originally described explicitly as finite state automata. Similar to reinforcement learning, learning automata algorithm also has the advantage of solving the problem when probability or rewards are unknown. The difference between learning automata and Q-learning is that they omit the memory of Q-values, but update the action probability directly to find the learning result. Learning automata is a learning scheme with a rigorous proof of convergence.

    In learning automata theory, a stochastic automaton to consist of:

  • a set x of possible inputs,
  • a set Φ = { Φ1, ..., Φs } of possible internal states,
  • a set α = { α1, ..., αr } of possible outputs, or actions, with r≤s,
  • an initial state probability vector p(0) = ≪ p1(0), ..., ps(0) ≫,
  • a computable function A which after each time step t generates p(t+1) from p(t), the current input, and the current state, and
  • a function G: Φ → α which generates the output at each time step.

    • The states of such an automaton correspond to the states of a "discrete-state discrete-parameter Markov process". At each time step t=0,1,2,3,..., the automaton reads an input from its environment, updates P(t) to P(t+1) by A, randomly chooses a successor state according to the probabilities P(t+1) and outputs the corresponding action. The automaton's environment, in turn, reads the action and sends the next input to the automaton.

    Category theoretic interpretation

    Other than the rewards, a Markov decision process ( S , A , P ) can be understood in terms of Category theory. Namely, let A denote the free monoid with generating set A. Let Dist denote the Kleisli category of the Giry monad. Then a functor A → D i s t encodes both the set S of states and the probability function P.

    In this way, Markov decision processes could be generalized from monoids (categories with one object) to arbitrary categories. One can call the result ( C , F : C → D i s t ) a context-dependent Markov decision process, because moving from one object to another in C changes the set of available actions and the set of possible states.

    Fuzzy Markov decision processes (FMDPs)

    In the MDPs, optimal policy is a policy which maximize the summation of future rewards. Therefore, optimal policy consist several actions which belong to a finite set of actions. In Fuzzy Markov decision processes (FMDPs), first, the value function is computed as regular MDPs i.e. with a finite set of actions; then, the policy is extracted by a fuzzy inference system. In other words, the value function is utilized as an input for the fuzzy inference system, and the policy is the output of the fuzzy inference system.

    Continuous-time Markov Decision Process

    In discrete-time Markov Decision Processes, decisions are made at discrete time intervals. However, for Continuous-time Markov Decision Processes, decisions can be made at any time the decision maker chooses. In comparison to discrete-time Markov Decision Process, Continuous-time Markov Decision Process can better model the decision making process for a system that has continuous dynamics, i.e., the system dynamics is defined by partial differential equations (PDEs).

    Definition

    In order to discuss the continuous-time Markov Decision Process, we introduce two sets of notations:

    If the state space and action space are finite,

  • S : State space;
  • A : Action space;
  • q ( i | j , a ) : S × A → △ S , transition rate function;
  • R ( i , a ) : S × A → R , a reward function.

    • If the state space and action space are continuous,

  • X : state space;
  • U : space of possible control;
  • f ( x , u ) : X × U → △ X , a transition rate function;
  • r ( x , u ) : X × U → R , a reward rate function such that r ( x ( t ) , u ( t ) ) d t = d R ( x ( t ) , u ( t ) ) , where R ( x , u ) is the reward function we discussed in previous case.

    • Problem

    Like the Discrete-time Markov Decision Processes, in Continuous-time Markov Decision Process we want to find the optimal policy or control which could give us the optimal expected integrated reward:

    max E u [ ∫ 0 ∞ γ t r ( x ( t ) , u ( t ) ) ) d t | x 0 ]

    Where 0 ≤ γ < 1

    Linear programming formulation

    If the state space and action space are finite, we could use linear programming to find the optimal policy, which was one of the earliest approaches applied. Here we only consider the ergodic model, which means our continuous-time MDP becomes an ergodic continuous-time Markov Chain under a stationary policy. Under this assumption, although the decision maker can make a decision at any time at the current state, he could not benefit more by taking more than one action. It is better for him to take an action only at the time when system is transitioning from the current state to another state. Under some conditions,(for detail check Corollary 3.14 of Continuous-Time Markov Decision Processes), if our optimal value function V ∗ is independent of state i , we will have the following inequality:

    g ≥ R ( i , a ) + ∑ j ∈ S q ( j | i , a ) h ( j ) ∀ i ∈ S a n d a ∈ A ( i )

    If there exists a function h , then V ¯ ∗ will be the smallest g satisfying the above equation. In order to find V ¯ ∗ , we could use the following linear programming model:

  • Primal linear program(P-LP)
    • Minimize g s.t g − ∑ j ∈ S q ( j | i , a ) h ( j ) ≥ R ( i , a ) ∀ i ∈ S , a ∈ A ( i )
  • Dual linear program(D-LP)
    • Maximize ∑ i ∈ S ∑ a ∈ A ( i ) R ( i , a ) y ( i , a ) s.t. ∑ i ∈ S ∑ a ∈ A ( i ) q ( j | i , a ) y ( i , a ) = 0 ∀ j ∈ S , ∑ i ∈ S ∑ a ∈ A ( i ) y ( i , a ) = 1 , y ( i , a ) ≥ 0 ∀ a ∈ A ( i ) a n d ∀ i ∈ S

    y ( i , a ) is a feasible solution to the D-LP if y ( i , a ) is nonnative and satisfied the constraints in the D-LP problem. A feasible solution y ∗ ( i , a ) to the D-LP is said to be an optimal solution if

    ∑ i ∈ S ∑ a ∈ A ( i ) R ( i , a ) y ∗ ( i , a ) ≥ ∑ i ∈ S ∑ a ∈ A ( i ) R ( i , a ) y ( i , a )

    for all feasible solution y ( i , a ) to the D-LP. Once we found the optimal solution y ∗ ( i , a ) , we could use those optimal solution to establish the optimal policies.

    Hamilton-Jacobi-Bellman equation

    In continuous-time MDP, if the state space and action space are continuous, the optimal criterion could be found by solving Hamilton-Jacobi-Bellman (HJB) partial differential equation. In order to discuss the HJB equation, we need to reformulate our problem

    V ( x ( 0 ) , 0 ) = max u ∫ 0 T r ( x ( t ) , u ( t ) ) d t + D [ x ( T ) ] s . t . d x ( t ) d t = f [ t , x ( t ) , u ( t ) ]

    D ( ⋅ ) is the terminal reward function, x ( t ) is the system state vector, u ( t ) is the system control vector we try to find. f ( ⋅ ) shows how the state vector change over time. Hamilton-Jacobi-Bellman equation is as follows:

    0 = max u ( r ( t , x , u ) + ∂ V ( t , x ) ∂ x f ( t , x , u ) )

    We could solve the equation to find the optimal control u ( t ) , which could give us the optimal value V ∗

    Application

    Continuous-time Markov decision processes have applications in queueing systems, epidemic processes, and population processes.

    Alternative notations

    The terminology and notation for MDPs are not entirely settled. There are two main streams — one focuses on maximization problems from contexts like economics, using the terms action, reward, value, and calling the discount factor β or γ , while the other focuses on minimization problems from engineering and navigation, using the terms control, cost, cost-to-go, and calling the discount factor α . In addition, the notation for the transition probability varies.

    In addition, transition probability is sometimes written P r ( s , a , s ′ ) , P r ( s ′ | s , a ) or, rarely, p s ′ s ( a ) .

    Constrained Markov Decision Processes

    Constrained Markov Decision Processes (CMDPs) are extensions to Markov Decision Process (MDPs). There are three fundamental differences between MDPs and CMDPs.

  • There are multiple costs incurred after applying an action instead of one.
  • CMDPs are solved with Linear Programs only, and Dynamic programming does not work.
  • The final policy depends on the starting state.

    • There are a number of applications for CMDPs. It is recently being used in motion planning scenarios in robotics.

    References

    Markov decision process Wikipedia
    (Text) CC BY-SA


    Similar Topics