 | ||
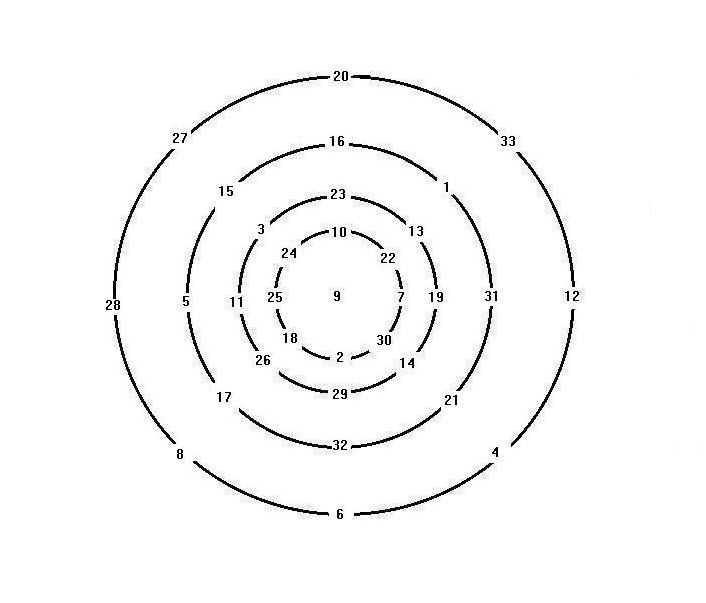
Magic circles were invented by the Song dynasty (960–1279) Chinese mathematician Yang Hui (c. 1238–1298). It is the arrangement of natural numbers on circles where the sum of the numbers on each circle and the sum of numbers on diameter are identical. One of his magic circles was constructed from 33 natural numbers from 1 to 33 arranged on four concentric circles, with 9 at the center.
Contents
Yang Hui magic circles
Yang Hui's magic circle series was published in his Xugu Zhaiqi Suanfa《續古摘奇算法》 (Sequel to Excerpts of Mathematical Wonders) of 1275. His magic circle series includes: magic 5 circles in square, 6 circles in ring, magic eight circle in square magic concentric circles, magic 9 circles in square.
Yang Hui magic concentric circle
Yang Hui's magic concentric circle has the following properties
Yang Hui magic eight circles in a square
64 numbers arrange in circles of eight numbers, total sum 2080, horizontal / vertical sum =260.
From NW corner clockwise direction, the sum of 8-number circles are:
Also the sum of the eight numbers along the WE/NS axis
Furthermore, the sum of the 16 numbers along the two diagonals equals to 2 times 260:
Yang Hui Magic Nine circles in a square
72 number from 1 to 72, arranged in nine circles of eight number circle in a square; with neighbouring numbers also forming four additional 8-number circles:
form out of the borders of the following 8-circles:
thus making a total of 13 8-circles in a square:
NW,N,NE,E,SE,S,SW,W,C(center),(NW,N,W,C),(NE,N,E,C),(SW,S,W,C),(SE,S,E,C)Ding Yidong magic circles
Ding Yidong was a mathematician contemporary with Yang Hui. In his magic circle with 6 rings, the unit numbers of the 5 outer rings, combined with the unit number of the center ring, form the following magic square:
Method of construction:
Let radial group 1 =1,11,21,31,41Let radial group 2=2,12,22,32,42Let radial group 3=3,13,23,33,43Let radial group 4=4,14,24,34,44Let radial group 6=6,16,26,36,46Let radial group 7=7,17,27,37,47Let radial group 8=8,18,28,38,48Let radial group 9=9,19,29,39,49Let center group =5,15,25,35,45Arrange group 1,2,3,4,6,7,9 radially such that
Cheng Dawei magic circles
Cheng Dawei, a mathematician in the Ming dynasty, in his book Suanfa Tongzong listed several magic circles
