 | ||
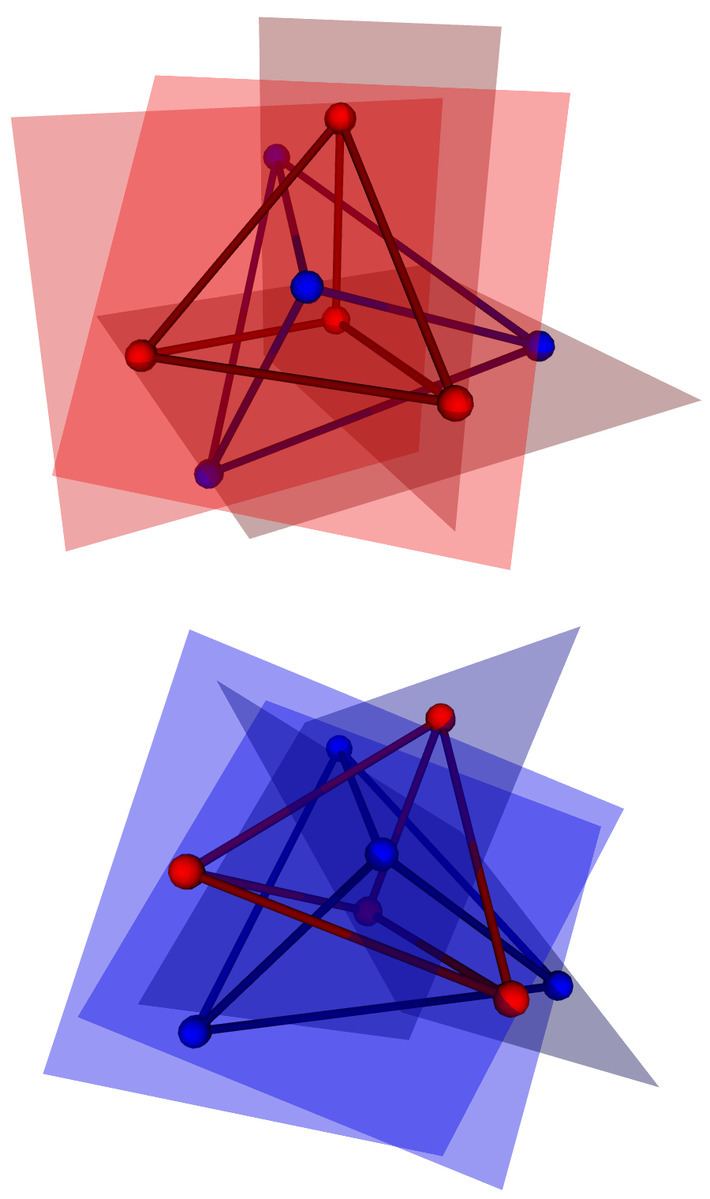
In geometry, the Möbius configuration or Möbius tetrads is a certain configuration in Euclidean space or projective space, consisting of two mutually inscribed tetrahedra: each vertex of one tetrahedron lies on a face plane of the other tetrahedron and vice versa. Thus, for the resulting system of eight points and eight planes, each point lies on four planes (the three planes defining it as a vertex of a tetrahedron and the fourth plane from the other tetrahedron that it lies on), and each plane contains four points (the three tetrahedron vertices of its face, and the vertex from the other tetrahedron that lies on it).
Contents
Möbius's theorem
The configuration is named after August Ferdinand Möbius, who in 1828 proved that, if two tetrahedra have the property that seven of their vertices lie on corresponding face planes of the other tetrahedron, then the eighth vertex also lies on the plane of its corresponding face, forming a configuration of this type. This incidence theorem is true more generally in a three-dimensional projective space if and only if Pappus's theorem holds for that space (Reidemeister, Schönhardt), and it is true for a three-dimensional space modeled on a division ring if and only if the ring satisfies the commutative law and is therefore a field (Al-Dhahir). By projective duality, Möbius' result is equivalent to the statement that, if seven of the eight face planes of two tetrahedra contain the corresponding vertices of the other tetrahedron, then the eighth face plane also contains the same vertex.
Construction
Coxeter (1950) describes a simple construction for the configuration. Beginning with an arbitrary point p in Euclidean space, let A, B, C, and D be four planes through p, no three of which share a common intersection line, and place the six points q, r, s, t, u, and v on the six lines formed by pairwise intersection of these planes in such a way that no four of these points are coplanar. For each of the planes A, B, C, and D, four of the seven points p, q, r, s, t, u, and v lie on that plane and three are disjointed from it; form planes A’, B’, C’, and D’ through the triples of points disjoint from A, B, C, and D respectively. Then, by the dual form of Möbius' theorem, these four new planes meet in a single point w. The eight points p, q, r, s, t, u, v, and w and the eight planes A, B, C, D, A’, B’, C’, and D’ form an instance of Möbius' configuration.
Related constructions
Hilbert & Cohn-Vossen (1952) state (without references) that there are five configurations having eight points and eight planes with four points on every plane and four planes through every point that are realisable in three-dimensional Euclidean space: such configurations have the shorthand notation
It is also stated that by Steinitz that the only
The Levi graph of the Möbius configuration has 16 vertices, one for each point or plane of the configuration, with an edge for every incident point-plane pair. It is isomorphic to the 16-vertex hypercube graph Q4. A closely related configuration, the Möbius–Kantor configuration formed by two mutually inscribed quadrilaterals, has the Möbius–Kantor graph, a subgraph of Q4, as its Levi graph.
