Lunar distance (navigation)

Purpose

In celestial navigation, knowledge of the time at Greenwich and the measured positions of one or more celestial objects allows the navigator to calculate latitude and longitude. Reliable marine chronometers were unavailable until the late 18th century and not affordable until the 19th century. After the method was first published in 1763 by British astronomer royal Nevil Maskelyne, for about a hundred years (until about 1850) mariners lacking a chronometer used the method of lunar distances to determine Greenwich time as a key step in determining longitude. Conversely, a mariner with a chronometer could check its accuracy using a lunar determination of Greenwich time. The method saw usage all the way up to the beginning of the 20th century on smaller vessels that could not afford a chronometer or had to rely on the this technique for correction of the chronometer.

Summary

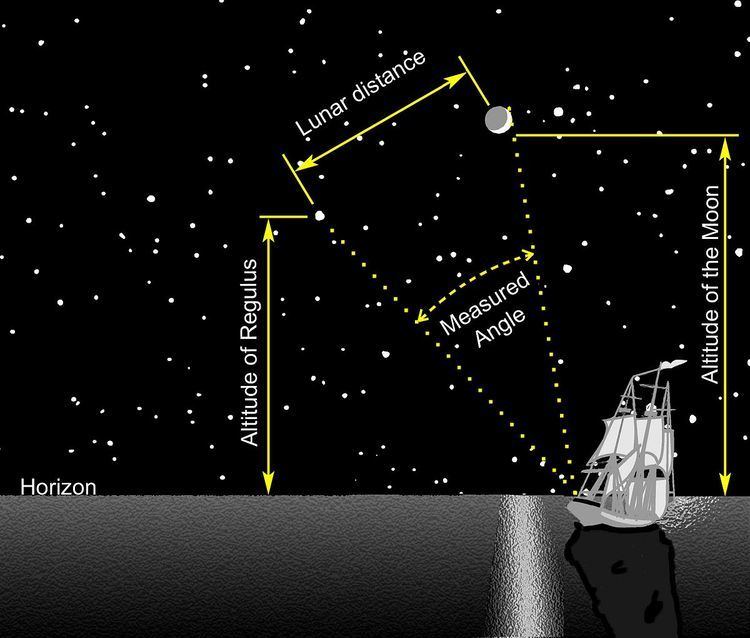
The method relies on the relatively quick movement of the moon across the background sky, completing a circuit of 360 degrees in 27.3 days. In an hour then, it will move about half a degree, roughly its own diameter, with respect to the background stars and the Sun. Using a sextant, the navigator precisely measures the angle between the moon and another body. That could be the Sun or one of a selected group of bright stars lying close to the Moon's path, near the ecliptic; Regulus was particularly commonly used. At that moment, anyone on the surface of the earth who can see the same two bodies will observe the same angle (after correcting for parallax error). The navigator then consults a prepared table of lunar distances and the times at which they will occur. By comparing the corrected lunar distance with the tabulated values, the navigator finds the Greenwich time for that observation. Knowing Greenwich time and local time, the navigator can work out longitude. Local time can be determined from a sextant observation of the altitude of the Sun or a star. Then the longitude (relative to Greenwich) is readily calculated from the difference between local time and Greenwich Time, at 15 degrees per hour.

In practice

Having measured the lunar distance and the heights of the two bodies, the navigator can find Greenwich time in three steps.

Step one – Preliminaries

Almanac tables predict lunar distances between the centre of the Moon and the other body (published between 1767 and 1906 in Britain). However, the observer cannot accurately find the centre of the Moon (or Sun, which was the most frequently used second object). Instead, lunar distances are always measured to the sharply lit, outer edge ("limb") of the Moon (or of the Sun). The first correction to the lunar distance is the distance between the limb of the Moon and its center. Since the Moon's apparent size varies with its varying distance from the Earth, almanacs give the Moon's and Sun's semidiameter for each day. Additionally the observed altitudes are cleared of dip and semidiameter.

Step two – Clearing

Clearing the lunar distance means correcting for the effects of parallax and atmospheric refraction on the observation. The almanac gives lunar distances as they would appear if the observer were at the center of a transparent Earth. Because the Moon is so much closer to the Earth than the stars are, the position of the observer on the surface of the Earth shifts the relative position of the Moon by up to an entire degree. The clearing correction for parallax and refraction is a relatively simple trigonometric function of the observed lunar distance and the altitudes of the two bodies. Navigators used collections of mathematical tables to work these calculations by any of dozens of distinct clearing methods.

Step three – Finding the time

The navigator, having cleared the lunar distance, now consults a prepared table of lunar distances and the times at which they will occur in order to determine the Greenwich time of the observation. These tables were the high tech wonder of their day. Predicting the position of the moon months in advance requires solving the three-body problem, since the earth, moon and sun were all involved. Euler developed the numerical method they used, called Euler's method, and received a grant from the Board of Longitude to carry out the computations.

Having found the (absolute) Greenwich time, the navigator either compares it with the observed local apparent time (a separate observation) to find longitude or compares it with the Greenwich time on a chronometer if one is available.

Errors

Almanac error

In the early days of lunars, predictions of the Moon's position were good to approximately half an arc-minute, a source of error of up to approximately 1 minute in Greenwich time, or one quarter degree of longitude. By 1810, the errors in the almanac predictions had been reduced to about one-quarter of a minute of arc. By about 1860 (after lunar distance observations had mostly faded into history), the almanac errors were finally reduced to less than the error margin of a sextant in ideal conditions (one-tenth of a minute of arc).

Lunar distance observation

The best sextants at the very beginning of the lunar distance era could indicate angle to one-sixth of a minute and later sextants (after c. 1800) measure angles with a precision of 0.1 minutes of arc, after the use of the vernier was popularized by its description in English in the book Navigatio Britannica published in 1750 by John Barrow, the mathematician and historian. In practice at sea, actual errors were somewhat larger. Experienced observers can typically measure lunar distances to within one-quarter of a minute of arc under favourable conditions, introducing an error of up to one quarter degree in longitude. Needless to say, if the sky is cloudy or the Moon is "New" (hidden close to the glare of the Sun), lunar distance observations could not be performed.

Total error

A lunar distance changes with time at a rate of roughly half a degree, or 30 arc-minutes, in an hour. The two sources of error, combined, typically amount to about one-half arc-minute in Lunar distance, equivalent to one minute in Greenwich time, which corresponds to an error of as much as one-quarter of a degree of Longitude, or about 15 nautical miles (28 km) at the equator.

In literature

Captain Joshua Slocum, in making the first solo circumnavigation in 1895–1898, somewhat anachronistically used the lunar method along with dead reckoning in his navigation. He comments in Sailing Alone Around the World on a sight taken in the South Pacific. After correcting an error he found in his log tables, the result was surprisingly accurate:

I found from the result of three observations, after long wrestling with lunar tables, that her longitude agreed within five miles of that by dead-reckoning. This was wonderful; both, however, might be in error, but somehow I felt confident that both were nearly true, and that in a few hours more I should see land; and so it happened, for then I made out the island of Nukahiva, the southernmost of the Marquesas group, clear-cut and lofty. The verified longitude when abreast was somewhere between the two reckonings; this was extraordinary. All navigators will tell you that from one day to another a ship may lose or gain more than five miles in her sailing-account, and again, in the matter of lunars, even expert lunarians are considered as doing clever work when they average within eight miles of the truth...

The result of these observations naturally tickled my vanity, for I knew it was something to stand on a great ship’s deck and with two assistants take lunar observations approximately near the truth. As one of the poorest of American sailors, I was proud of the little achievement alone on the sloop, even by chance though it may have been...

The work of the lunarian, though seldom practised in these days of chronometers, is beautifully edifying, and there is nothing in the realm of navigation that lifts one’s heart up more in adoration.