 | ||
Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through, is emitted or reflected from a particular area, and falls within a given solid angle. The SI unit for luminance is candela per square metre (cd/m2). A non-SI term for the same unit is the "nit". The CGS unit of luminance is the stilb, which is equal to one candela per square centimetre or 10 kcd/m2.
Contents
Explanation
Luminance is often used to characterize emission or reflection from flat, diffuse surfaces. The luminance indicates how much luminous power will be detected by an eye looking at the surface from a particular angle of view. Luminance is thus an indicator of how bright the surface will appear. In this case, the solid angle of interest is the solid angle subtended by the eye's pupil. Luminance is used in the video industry to characterize the brightness of displays. A typical computer display emits between 50 and 7002300000000000000♠300 cd/m2. The sun has luminance of about 7009160000000000000♠1.6×109 cd/m2 at noon.
Luminance is invariant in geometric optics. This means that for an ideal optical system, the luminance at the output is the same as the input luminance. For real, passive, optical systems, the output luminance is at most equal to the input. As an example, if one uses a lens to form an image that is smaller than the source object, the luminous power is concentrated into a smaller area, meaning that the illuminance is higher at the image. The light at the image plane, however, fills a larger solid angle so the luminance comes out to be the same assuming there is no loss at the lens. The image can never be "brighter" than the source.
Definition
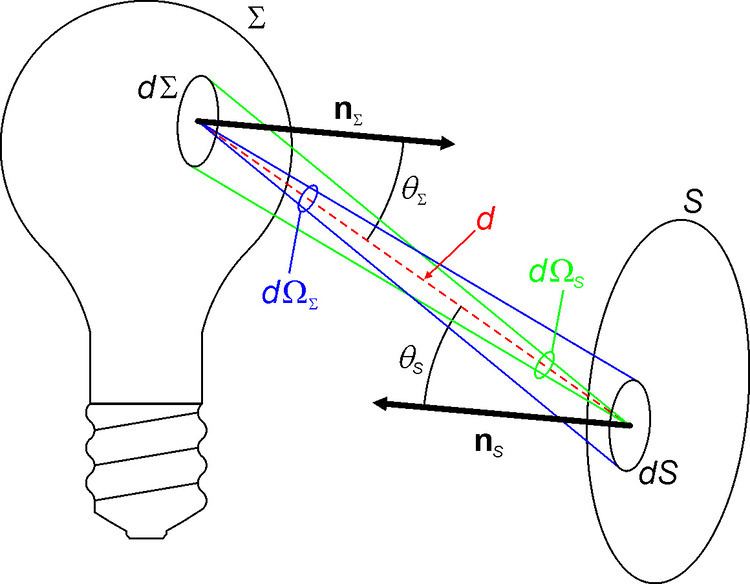
The luminance of a specified point of a light source, in a specified direction, is defined by the derivative
where
If light travels through a lossless medium, the luminance does not change along a given light ray. As the ray crosses an arbitrary surface S, the luminance is given by
where
More generally, the luminance along a light ray can be defined as
where
Relation to Illuminance
The luminance of a reflecting surface is related to the illuminance it receives:
where the integral covers all the directions of emission ΩΣ, and
In the case of a perfectly diffuse reflector (also called a Lambertian reflector), the luminance is isotropic, per Lambert's cosine law. Then the relationship is simply
Units
A variety of units have been used for luminance, besides the candela per square metre.
One candela per square metre is equal to:
Health effects
Retinal damage can occur when the eye is exposed to high luminance. Damage can occur due to local heating of the retina. Photochemical effects can also cause damage, especially at short wavelengths.
