 | ||
Low-dimensional chaos in stellar pulsations is the current interpretation of an established phenomenon. The light curves of intrinsic variable stars with large amplitudes have been known for centuries to exhibit behavior that goes from extreme regularity, as for the classical Cepheids and the RR Lyrae stars, to extreme irregularity, as for the so-called Irregular variables. In the Population II stars this irregularity gradually increases from the low period W Virginis variables through the RV Tauri variables into the regime of the semiregular variables.
Contents
Regular behavior of the Cepheids
The regular behavior of the Cepheids has been successfully modeled with numerical hydrodynamics since the 1960s, and from a theoretical point of view it is easily understood as due to the presence of center manifold which arises because of the weakly dissipative nature of the dynamical system. This, and the fact that the pulsations are weakly nonlinear, allows a description of the system in terms of amplitude equations and a construction of the bifurcation diagram (see also bifurcation theory) of the possible types of pulsation (or limit cycles), such fundamental mode pulsation, first or second overtone pulsation, or more complicated, double-mode pulsations in which several modes are excited with constant amplitudes. The boundaries of the instability strip where pulsation sets in during the star's evolution correspond to a Hopf bifurcation.
Irregularity of Population II stars
In contrast, the irregularity of the large amplitude Population II stars is more challenging to explain. The variation of the pulsation amplitude over one period implies large dissipation, and therefore there exists no center manifold. Various mechanisms have been proposed, but are found lacking. One, suggests the presence of several closely spaced pulsation frequencies that would beat against each other, but no such frequencies exist in the appropriate stellar models. Another, more interesting suggestion is that the variations are of a stochastic nature, but no mechanism has been proposed or exists that could provide the energy for such large observed amplitude variations. It is now established that the mechanism behind the irregular light curves is an underlying low dimensional chaotic dynamics (see also Chaos theory). This conclusion is based on two types of studies.
Numerical hydrodynamics simulations
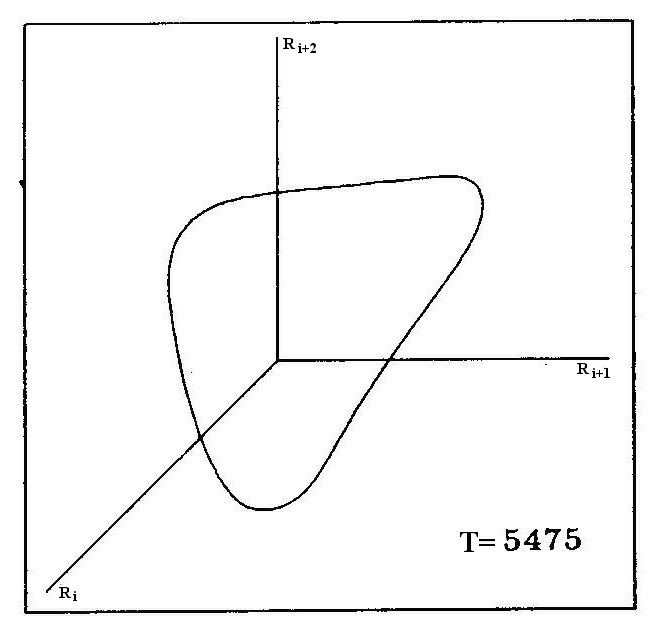
The numerical computations of the pulsations of sequences of W Virginis stellar models exhibit two approaches to irregular behavior that are a clear signature of low dimensional chaos. The first indication comes from first return maps in which one plots one maximum radius, or any other suitable variable, versus the next one. The sequence of models shows a period doubling bifurcation, or cascade, leading to chaos. The near quadratic shape of the map is indicative of chaos and implies an underlying horseshoe map Other sequences of models follow a somewhat different route, but also to chaos, namely the Pommeau-Manneville or tangent bifurcation route.
The following shows a similar visualization of the period doubling cascade to chaos for a sequence of stellar models that differ by their average surface temperature T. The graph shows triplets of values of the stellar radius (Ri, Ri+1, Ri+2) where the indices i, i+1, i+2 indicate successive time intervals.
The presence of low dimensional chaos is also confirmed by another, more sophisticated, analysis of the model pulsations which extracts the lowest unstable periodic orbits and examines their topological organization (twisting). The underlying attractor is found to be banded like the Roessler attractor, with however an additional twist in the band.
Global flow reconstruction from observed light curves
The method of global flow reconstruction uses a single observed signal {si} to infer properties of the dynamical system that generated it. First N-dimensional 'vectors' Si=(si,si-1,si-2,...,si-N+1) are constructed. The next step consists in finding an expression for the nonlinear evolution operator M that takes the system from time i to time i+1, i.e. Si+1= M (Si). Takens' theorem guarantees that under very general circumstances the topological properties of this reconstructed evolution operator are the same as that of the physical system, provided the embedding dimension N is large enough. Thus from the knowledge of a single observed variable one can infer properties about the real physical system which is governed by a number of independent variables.
This approach has been applied to the AAVSO data for the star R Scuti It could be inferred that the irregular pulsations of this star arise from an underlying 4-dimensional dynamics. Phrased differently this says that from any 4 neighboring observations one can predict the next one. From a physical point of view it says that there are 4 independent variables that describe the dynamic of the system. The method of false nearest neighbors corroborates an embedding dimension of 4. The fractal dimension of the dynamics of R Scuti as inferred from the computed Lyapunov exponents lies between 3.1 and 3.2.
From an analysis of the fixed points of the evolution operator a nice physical picture can be inferred, namely that the pulsations arise from the excitation of an unstable pulsation mode that couples nonlinearly to a second, stable pulsation mode which is in a 2:1 resonance with the first one, a scenario described by the Shilnikov theorem "[14]".
This resonance mechanism is not limited to R Scuti, but has been found to hold for several other stars for which the observational data are sufficiently good.
