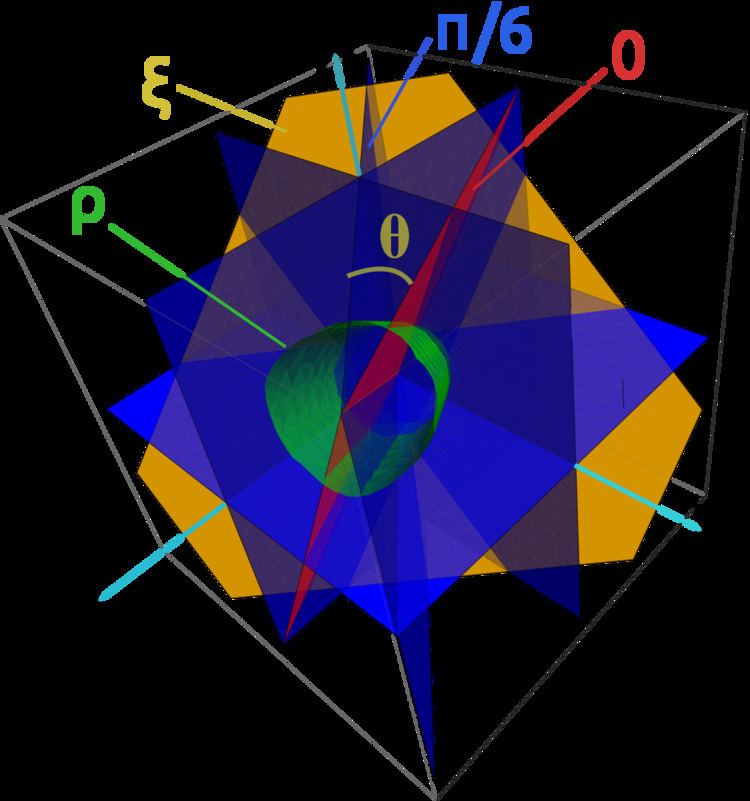
Lode coordinates
(
z
,
r
,
θ
)
or Haigh-Westergaard coordinates
(
ξ
,
ρ
,
θ
)
. are a set of tensor invariants that span the space of real, symmetric, second-order, 3-dimensional tensors and are isomorphic with respect to principal stress space. This right-handed orthogonal coordinate system is named in honor of the German scientist Dr. Walter Lode because of his seminal paper written in 1926 describing the effect of the middle principal stress on metal plasticity. Other examples of sets of tensor invariants are the set of principal stresses
(
σ
1
,
σ
2
,
σ
3
)
or the set of mechanics invariants
(
I
1
,
J
2
,
J
3
)
. The Lode coordinate system can be described as a cylindrical coordinate system within principal stress space with a coincident origin and the z-axis parallel to the vector
(
σ
1
,
σ
2
,
σ
3
)
=
(
1
,
1
,
1
)
.
The Lode coordinates are most easily computed using the mechanics invariants. These invariants are a mixture of the invariants of the Cauchy stress tensor,
σ
, and the stress deviator,
s
, and are given by
I
1
=
t
r
(
σ
)
J
2
=
1
2
[
tr
(
σ
2
)
−
1
3
tr
(
σ
)
2
]
=
1
2
t
r
(
s
⋅
s
)
=
1
2
∥
s
∥
2
J
3
=
d
e
t
(
s
)
=
1
3
t
r
(
s
⋅
s
⋅
s
)
which can be written equivalently in Einstein notation
I
1
=
σ
k
k
J
2
=
1
2
[
tr
(
σ
2
)
−
1
3
tr
(
σ
)
2
]
=
1
2
s
i
j
s
j
i
=
1
2
s
i
j
s
i
j
J
3
=
1
6
ϵ
i
j
k
ϵ
p
q
r
σ
i
p
σ
j
q
σ
k
r
=
1
3
s
i
j
s
j
k
s
k
i
where
ϵ
is the Levi-Civita symbol (or permutation symbol) and the last two forms for
J
2
are equivalent because
s
is symmetric (
s
i
j
=
s
j
i
).
The gradients of these invariants can be calculated by
∂
I
1
∂
σ
=
I
∂
J
2
∂
σ
=
s
=
σ
−
t
r
(
σ
)
3
I
∂
J
3
∂
σ
=
T
=
s
⋅
s
−
2
J
2
3
I
where
I
is the 3x3 identity matrix and
T
is called the Hill tensor.
The
z
-coordinate is found by calculating the magnitude of the orthogonal projection of the stress state onto the hydrostatic axis.
z
=
E
z
:
σ
=
t
r
(
σ
)
3
=
I
1
3
where
E
z
=
I
∥
I
∥
=
I
3
is the unit normal in the direction of the hydrostatic axis.
The
r
-coordinate is found by calculating the magnitude of the stress deviator (the orthogonal projection of the stress state into the deviatoric plane).
r
=
E
r
:
σ
=
∥
s
∥
=
2
J
2
where
E
r
=
s
∥
s
∥
is a unit tensor in the direction of the radial component.
The Lode angle can be considered, rather loosely, a measure of loading type. The Lode angle varies with respect to the middle eigenvalue of the stress. There are many definitions of Lode angle that each utilize different trigonometric functions: the positive sine, negative sine, and positive cosine (here denoted
θ
s
,
θ
¯
s
, and
θ
c
, respectively)
sin
(
3
θ
s
)
=
−
sin
(
3
θ
¯
s
)
=
cos
(
3
θ
c
)
=
J
3
2
(
3
J
2
)
3
/
2
and are related by
θ
s
=
π
6
−
θ
c
θ
s
=
−
θ
¯
s
These definitions are all defined for a range of
π
/
3
.
The unit normal in the angular direction which completes the orthonormal basis can be calculated for
θ
s
and
θ
c
using
E
θ
s
=
T
/
∥
T
∥
−
sin
(
3
θ
s
)
E
z
cos
(
3
θ
s
)
E
θ
c
=
T
/
∥
T
∥
−
cos
(
3
θ
c
)
E
z
sin
(
3
θ
s
)
.
The meridional profile is a 2D plot of
(
z
,
r
)
holding
θ
constant and is sometimes plotted using scalar multiples of
(
z
,
r
)
. It is commonly used to demonstrate the pressure dependence of a yield surface or the pressure-shear trajectory of a stress path. Because
r
is non-negative the plot usually omits the negative portion of the
r
-axis, but can be included to illustrate effects at opposing Lode angles (usually triaxial extension and triaxial compression).
One of the benefits of plotting the meridional profile with
(
z
,
r
)
is that it is a geometrically accurate depiction of the yield surface. If a non-isomorphic pair is used for the meridional profile then the normal to the yield surface will not appear normal in the meridional profile. Any pair of coordinates that differ from
(
z
,
r
)
by constant multiples of equal absolute value are also isomorphic with respect to principal stress space. As an example, pressure
p
=
−
I
1
/
3
and the Von Mises stress
σ
v
=
3
J
2
are not an isomorphic coordinate pair and, therefore, distort the yield surface because
p
=
−
1
3
z
σ
v
=
3
2
r
and, finally,
|
−
1
/
3
|
≠
|
3
/
2
|
.
The octahedral profile is a 2D plot of
(
r
,
θ
)
holding
z
constant. Plotting the yield surface in the octahedral plane demonstrates the level of Lode angle dependence. The octahedral plane is sometimes referred to as the 'pi plane' or 'deviatoric plane'.
The octahedral profile is not necessarily constant for different values of pressure with the notable exceptions of the von Mises yield criterion and the Tresca yield criterion which are constant for all values of pressure.
The term Haigh-Westergaard space is ambiguously used in the literature to mean both the Cartesian principal stress space and the cylindrical Lode coordinate space