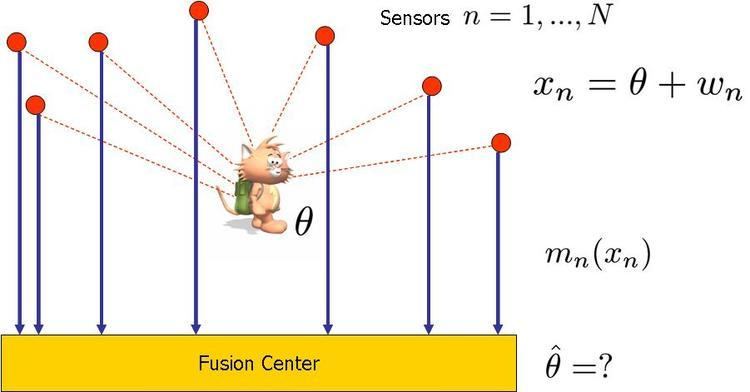
Location estimation in wireless sensor networks is the problem of estimating the location of an object from a set of noisy measurements. These measurements are acquired in a distributed manner by a set of sensors.
Many civilian and military applications require monitoring that can identify objects in a specific area, such as monitoring the front entrance of a private house by a single camera. Monitored areas that are large relative to objects of interest often require multiple sensors (e.g., infra-red detectors) at multiple locations. A centralized observer or computer application monitors the sensors. The communication to power and bandwidth requirements call for efficient design of the sensor, transmission, and processing.
The CodeBlue system of Harvard university is an example where a vast number of sensors distributed among hospital facilities allow staff to locate a patient in distress. In addition, the sensor array enables online recording of medical information while allowing the patient to move around. Military applications (e.g. locating an intruder into a secured area) are also good candidates for setting a wireless sensor network.
Let θ denote the position of interest. A set of N sensors acquire measurements x n = θ + w n contaminated by an additive noise w n owing some known or unknown probability density function (PDF). The sensors transmit measurements to a central processor. The n th sensor encodes x n by a function m n ( x n ) . The application processing the data applies a pre-defined estimation rule θ ^ = f ( m 1 ( x 1 ) , ⋅ , m N ( x N ) ) . The set of message functions m n , 1 ≤ n ≤ N and the fusion rule f ( m 1 ( x 1 ) , ⋅ , m N ( x N ) ) are designed to minimize estimation error. For example: minimizing the mean squared error (MSE), E ∥ θ − θ ^ ∥ 2 .
Ideally, sensors transmit their measurements x n right to the processing center, that is m n ( x n ) = x n . In this settings, the maximum likelihood estimator (MLE) θ ^ = 1 N ∑ n = 1 N x n is an unbiased estimator whose MSE is E ∥ θ − θ ^ ∥ 2 = var ( θ ^ ) = σ 2 N assuming a white Gaussian noise w n ∼ N ( 0 , σ 2 ) . The next sections suggest alternative designs when the sensors are bandwidth constrained to 1 bit transmission, that is m n ( x n ) =0 or 1.
We begin with an example of a Gaussian noise w n ∼ N ( 0 , σ 2 ) , in which a suggestion for a system design is as follows
m n ( x n ) = I ( x n − τ ) = { 1 x n > τ 0 x n ≤ τ θ ^ = τ − F − 1 ( 1 N ∑ n = 1 N m n ( x n ) ) , F ( x ) = 1 2 π σ ∫ x ∞ e − w 2 / 2 σ 2 d w Here τ is a parameter leveraging our prior knowledge of the approximate location of θ . In this design, the random value of m n ( x n ) is distributed Bernoulli~ ( q = F ( τ − θ ) ) . The processing center averages the received bits to form an estimate q ^ of q , which is then used to find an estimate of θ . It can be verified that for the optimal (and infeasible) choice of τ = θ the variance of this estimator is π σ 2 4 which is only π / 2 times the variance of MLE without bandwidth constraint. The variance increases as τ deviates from the real value of θ , but it can be shown that as long as | τ − θ | ∼ σ the factor in the MSE remains approximately 2. Choosing a suitable value for τ is a major disadvantage of this method since our model does not assume prior knowledge about the approximated location of θ . A coarse estimation can be used to overcome this limitation. However, it requires additional hardware in each of the sensors.
A system design with arbitrary (but known) noise PDF can be found in. In this setting it is assumed that both θ and the noise w n are confined to some known interval [ − U , U ] . The estimator of also reaches an MSE which is a constant factor times σ 2 N . In this method, the prior knowledge of U replaces the parameter τ of the previous approach.
A noise model may be sometimes available while the exact PDF parameters are unknown (e.g. a Gaussian PDF with unknown σ ). The idea proposed in for this setting is to use two thresholds τ 1 , τ 2 , such that N / 2 sensors are designed with m A ( x ) = I ( x − τ 1 ) , and the other N / 2 sensors use m B ( x ) = I ( x − τ 2 ) . The processing center estimation rule is generated as follows:
q ^ 1 = 2 N ∑ n = 1 N / 2 m A ( x n ) , q ^ 2 = 2 N ∑ n = 1 + N / 2 N m B ( x n ) θ ^ = F − 1 ( q ^ 2 ) τ 1 − F − 1 ( q ^ 1 ) τ 2 F − 1 ( q ^ 2 ) − F − 1 ( q ^ 1 ) , F ( x ) = 1 2 π ∫ x ∞ e − v 2 / 2 d w As before, prior knowledge is necessary to set values for τ 1 , τ 2 to have an MSE with a reasonable factor of the unconstrained MLE variance.
We now describe the system design of for the case that the structure of the noise PDF is unknown. The following model is considered for this scenario:
x n = θ + w n , n = 1 , … , N θ ∈ [ − U , U ] w n ∈ P , that is : w n is bounded to [ − U , U ] , E ( w n ) = 0 In addition, the message functions are limited to have the form
m n ( x n ) = { 1 x ∈ S n 0 x ∉ S n where each S n is a subset of [ − 2 U , 2 U ] . The fusion estimator is also restricted to be linear, i.e. θ ^ = ∑ n = 1 N α n m n ( x n ) .
The design should set the decision intervals S n and the coefficients α n . Intuitively, we would allocate N / 2 sensors to encode the first bit of θ by setting their decision interval to be [ 0 , 2 U ] , then N / 4 sensors would encode the second bit by setting their decision interval to [ − U , 0 ] ∪ [ U , 2 U ] and so on. It can be shown that these decision intervals and the corresponding set of coefficients α n produce a universal δ -unbiased estimator, which is an estimator satisfying | E ( θ − θ ^ ) | < δ for every possible value of θ ∈ [ − U , U ] and for every realization of w n ∈ P . In fact, this intuitive design of the decision intervals is also optimal in the following sense. The above design requires N ≥ ⌈ log 8 U δ ⌉ to satisfy the universal δ -unbiased property while theoretical arguments show that an optimal (and a more complex) design of the decision intervals would require N ≥ ⌈ log 2 U δ ⌉ , that is: the number of sensors is nearly optimal. It is also argued in that if the targeted MSE E ∥ θ − θ ^ ∥ ≤ ϵ 2 uses a small enough ϵ , then this design requires a factor of 4 in the number of sensors to achieve the same variance of the MLE in the unconstrained bandwidth settings.
The design of the sensor array requires optimizing the power allocation as well as minimizing the communication traffic of the entire system. The design suggested in incorporates probabilistic quantization in sensors and a simple optimization program that is solved in the fusion center only once. The fusion center then broadcasts a set of parameters to the sensors that allows them to finalize their design of messaging functions m n ( ⋅ ) as to meet the energy constraints. Another work employs a similar approach to address distributed detection in wireless sensor arrays.