Linear dynamical system

Introduction

In a linear dynamical system, the variation of a state vector (an N -dimensional vector denoted x ) equals a constant matrix (denoted A ) multiplied by x . This variation can take two forms: either as a flow, in which x varies continuously with time

or as a mapping, in which x varies in discrete steps

These equations are linear in the following sense: if x ( t ) and y ( t ) are two valid solutions, then so is any linear combination of the two solutions, e.g., z ( t )   = d e f   α x ( t ) + β y ( t ) where α and β are any two scalars. The matrix A need not be symmetric.

Linear dynamical systems can be solved exactly, in contrast to most nonlinear ones. Occasionally, a nonlinear system can be solved exactly by a change of variables to a linear system. Moreover, the solutions of (almost) any nonlinear system can be well-approximated by an equivalent linear system near its fixed points. Hence, understanding linear systems and their solutions is a crucial first step to understanding the more complex nonlinear systems.

Solution of linear dynamical systems

If the initial vector x 0   = d e f   x ( t = 0 ) is aligned with a right eigenvector r k of the matrix A , the dynamics are simple

where λ k is the corresponding eigenvalue; the solution of this equation is

as may be confirmed by substitution.

If A is diagonalizable, then any vector in an N -dimensional space can be represented by a linear combination of the right and left eigenvectors (denoted l k ) of the matrix A .

Therefore, the general solution for x ( t ) is a linear combination of the individual solutions for the right eigenvectors

Similar considerations apply to the discrete mappings.

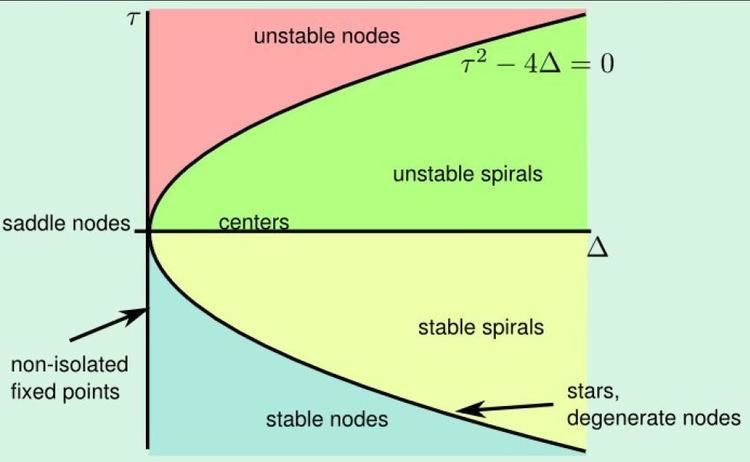
Classification in two dimensions

The roots of the characteristic polynomial det(A - λI) are the eigenvalues of A. The sign and relation of these roots, λ n , to each other may be used to determine the stability of the dynamical system

For a 2-dimensional system, the characteristic polynomial is of the form λ 2 − τ λ + Δ = 0 where τ is the trace and Δ is the determinant of A. Thus the two roots are in the form:

Note also that Δ = λ 1 λ 2 and τ = λ 1 + λ 2 . Thus if Δ < 0 then the eigenvalues are of opposite sign, and the fixed point is a saddle. If Δ > 0 then the eigenvalues are of the same sign. Therefore, if τ > 0 both are positive and the point is unstable, and if τ < 0 then both are negative and the point is stable. The discriminant will tell you if the point is nodal or spiral (i.e. if the eigenvalues are real or complex).