Supriya Ghosh (Editor)

Limiting parallel

Updated on
Edit
Like
Comment
Share on FacebookTweet on TwitterShare on LinkedInShare on Reddit
Limiting parallel

In neutral or absolute geometry, and in hyperbolic geometry, there may be many lines parallel to a given line l through a point P not on line R ; however, in the plane, two parallels may be closer to l than all others (one in each direction of R ).

Contents

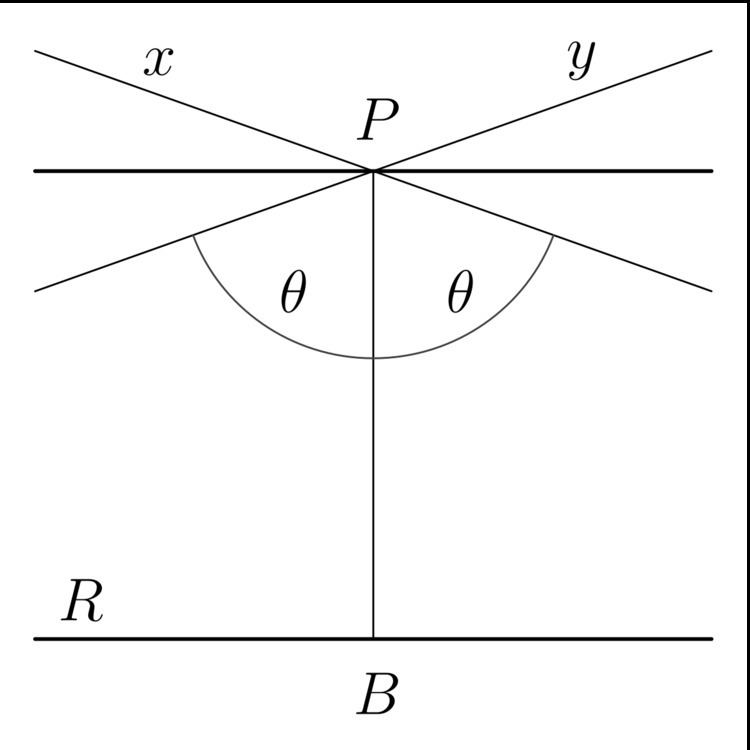
Thus it is useful to make a new definition concerning parallels in neutral geometry. If there are closest parallels to a given line they are known as the limiting parallel, asymptotic parallel or horoparallel (horo from Greek: ὅριον — border).

For rays, the relation of limiting parallel is an equivalence relation, which includes the equivalence relation of being coterminal.

Limiting parallels may form two, or three sides of a limit triangle.

Definition

A ray A a is a limiting parallel to a ray B b if they are coterminal or if they lie on distinct lines not equal to the line A B , they do not meet, and every ray in the interior of the angle B A a meets the ray B b .

Properties

Distinct lines carrying limiting parallel rays do not meet.

Proof

Suppose that the lines carrying distinct parallel rays met. By definition the cannot meet on the side of A B which either a is on. Then they must meet on the side of A B opposite to a , call this point C . Thus ∠ C A B + ∠ C B A < 2  right angles ⇒ ∠ a A B + ∠ b B A > 2  right angles . Contradiction.

References

Limiting parallel Wikipedia
(Text) CC BY-SA