 | ||
The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform (DWT). In an implementation, it is often worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform. This is then called the second generation wavelet transform. The technique was introduced by Wim Sweldens.
Contents
- Basics
- CDF 97 filter
- Perfect reconstruction
- Speedup
- Non linearities
- Increasing vanishing moments stability and regularity
- Generalized Lifting
- Applications
- References
The lifting scheme factorizes any discrete wavelet transform with finite filters into a series of elementary convolution operators, so-called lifting steps, which reduces the number of arithmetic operations by nearly a factor two. Treatment of signal boundaries is also simplified.
The discrete wavelet transform applies several filters separately to the same signal. In contrast to that, for the lifting scheme, the signal is divided like a zipper. Then a series of convolution-accumulate operations across the divided signals is applied.
Basics
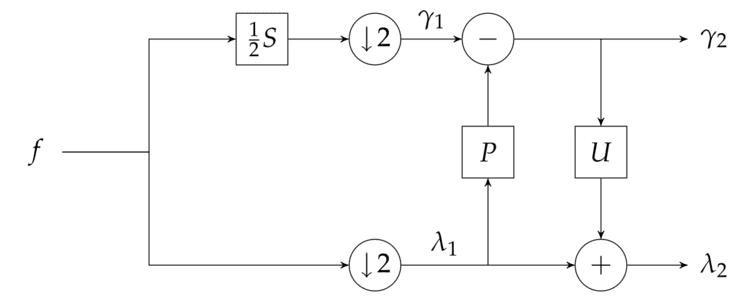
The simplest version of a forward wavelet transform expressed in the lifting scheme is shown in the figure.
As mentioned above the lifting scheme is an alternative technique for performing the DWT using biorthogonal wavelets. In order to perform the DWT using the lifting scheme, the corresponding lifting and scaling steps must be derived from the biorthogonal wavelets. The analysis filters (
The polyphase matrix is a 2 × 2 matrix containing the analysis low-pass and high-pass filters each split up into their even and odd polynomial coefficients and normalized. From here the matrix is factored into a series of 2 × 2 upper and lower triangular matrices each with diagonal entries equal to 1. The upper triangular matrices contain the coefficients for the predict steps and the lower triangular matrices contain the coefficients for the update steps. A matrix consisting of all zeros with the exception of the diagonal values may be extracted to derive the scaling step coefficients. The polyphase matrix is factored into the form
An example of a more complicated extraction having multiple predict and update steps as well as scaling steps is shown below;
According to matrix theory, any matrix having polynomial entries and a determinant of 1 can be factored as described above. Therefore every wavelet transform with finite filters can be decomposed into a series of lifting and scaling steps. Daubechies and Sweldens discuss lifting step extraction in further detail.
CDF 9/7 filter
A total of four lifting steps are required, two predict and two update steps, to perform the CDF 9/7 transform. The lifting factorization leads to the following sequence of filtering steps.
Perfect reconstruction
Every transform by the lifting scheme can be inverted. Every perfect reconstruction filter bank can be decomposed into lifting steps by the Euclidean algorithm. That is, "lifting decomposable filter bank" and "perfect reconstruction filter bank" denotes the same. Every two perfect reconstructable filter banks can be transformed into each other by a sequence of lifting steps. For a better understanding, if
Speedup
Speedup by a factor of two. This is only possible because lifting is restricted to perfect reconstruction filter banks. That is, lifting somehow squeezes out redundancies caused by perfect reconstruction.
The transformation can be performed immediately in the memory of the input data (in place, in situ) with only constant memory overhead.
Non-linearities
The convolution operations can be replaced by any other operation. For perfect reconstruction only the invertibility of the addition operation is relevant. This way rounding errors in convolution can be tolerated and bit-exact reconstruction is possible. However, the numeric stability may be reduced by the non-linearities. This must be respected if the transformed signal is processed like in lossy compression. Although every reconstructable filter bank can be expressed in terms of lifting steps, a general description of the lifting steps is not obvious from a description of a wavelet family. However, for instance, for simple cases of the Cohen-Daubechies-Feauveau wavelet, there is an explicit formula for their lifting steps.
Increasing vanishing moments, stability, and regularity
A lifting modifies biorthogonal filters in order to increase the number of vanishing moments of the resulting biorthogonal wavelets, and hopefully their stability and regularity. Increasing the number of vanishing moments decreases the amplitude of wavelet coefficients in regions where the signal is regular, which produces a more sparse representation. However, increasing the number of vanishing moments with a lifting also increases the wavelet support, which is an adverse effect that increases the number of large coefficients produced by isolated singularities. Each lifting step maintains the filter biorthogonality but provides no control on the Riesz bounds and thus on the stability of the resulting wavelet biorthogonal basis. When a basis is orthogonal then the dual basis is equal to the original basis. Having a dual basis that is similar to the original basis is, therefore, an indication of stability. As a result, stability is generally improved when dual wavelets have as much vanishing moments as original wavelets and a support of similar size. This is why a lifting procedure also increases the number of vanishing moments of dual wavelets. It can also improve the regularity of the dual wavelet. A lifting design is computed by adjusting the number of vanishing moments. The stability and regularity of the resulting biorthogonal wavelets are measured a posteriori, hoping for the best. This is the main weakness of this wavelet design procedure.
Generalized Lifting
The generalized lifting scheme is a derivative of the lifting scheme, in which the addition and subtraction operations are absorbed into the update and prediction steps, respectively. These steps can be any (invertible) mapping, leading to a more general lifting scheme.
